Reference
https://iai.postech.ac.kr/teaching/machine-learning
https://iai.postech.ac.kr/teaching/deep-learning
위 링크의 강의 내용에 기반하여 중요하거나 이해가 어려웠던 부분들을 정리하여 작성하였고,
모든 강의 슬라이드의 인용은 저작권자의 허가를 받았습니다.
또한, 모든 내용은 아래 Notion에서 더 편하게 확인하실 수 있습니다.
>>노션 링크<<
Keywords
- Autoencoder
- Dim. Reduction
- AE as Generative Model
Autoencoder

이미 앞 장(ML)에서 Unsupervised Learning이 무엇인지, 그리고 Dimesional Reduction과 그 방법 중 하나인 PCA에 대해서 학습하였다.

Autoencoder는 간단히 말해서 그러한 Unsupervised Learning (그 중 Dimensional Reduction)의 Deep Learning 버전이라고 생각할 수 있다.
Autoencoder는 또한 “Input을 output으로 copy하는 것을 학습하는 NN” 과 같이 정의할 수 있다.
그 NN은 두 개의 부분, encoder와 decoder로 나눠져 있는데, network의 두 부분 (encoder/decoder)를 거쳐 input을 output으로 재구성하는 과정을 거치게 되는 것이다. (input을 output으로 copy한다는 말의 뜻을 어렴풋이 이해할 수 있을 것이다. 더 정확하게 이해하려면 다음 설명을 보자.)
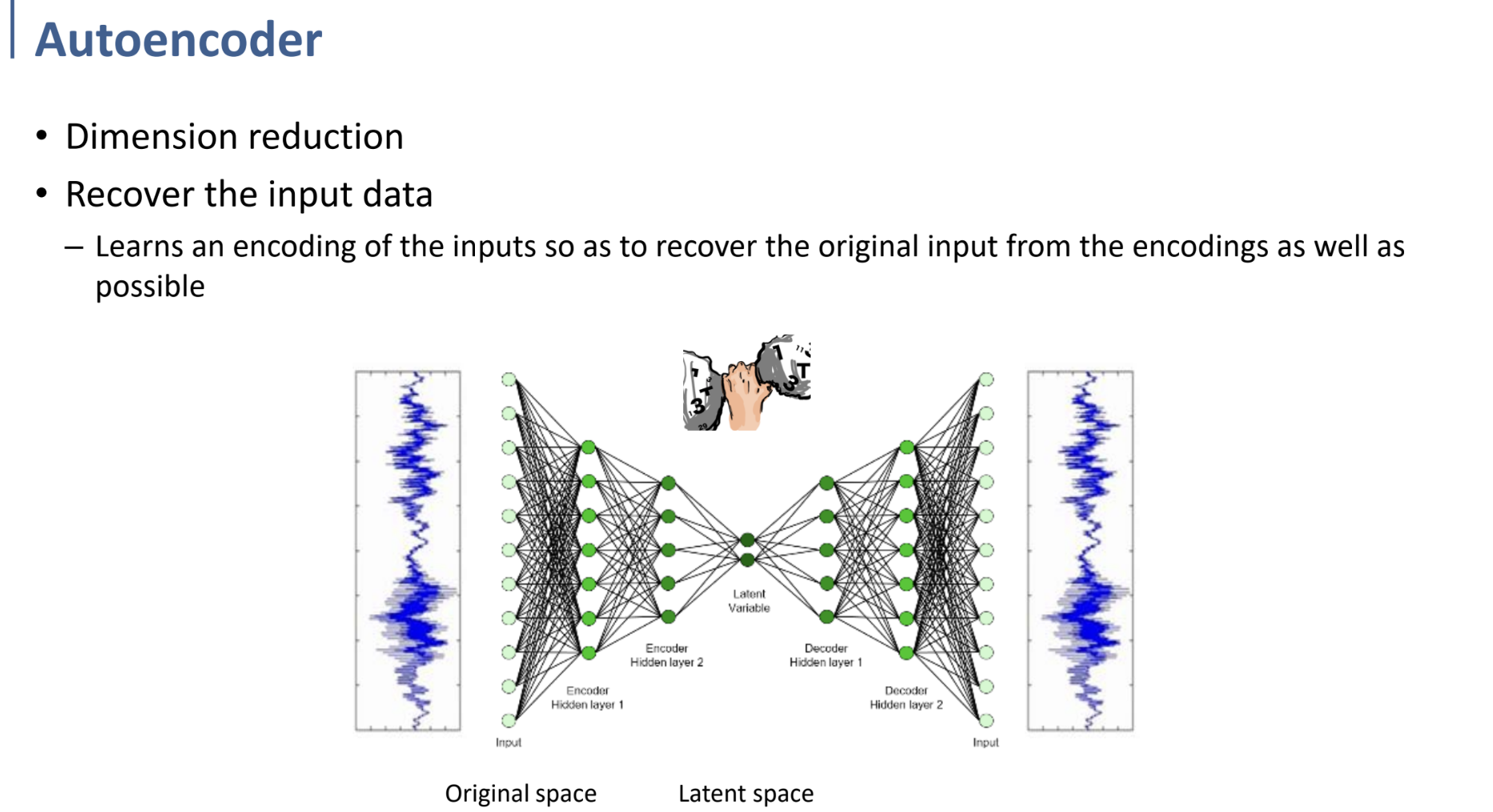
위의 사진에서와 같이, Input을 더 낮은 차원으로 압축하고 (encoding), 다시 그것을 복원하는 (decoding) 과정을 학습하는 것이다.
이렇게 학습하는 과정에서 이 Network를 거친 output이 최대한 input과 비슷해지도록 학습하려면, encoding 과정에서 dim. reduction이 일어날 때 최대한 정보 손실이 적도록 하여 encoding되어야 할 것이다.
Original space → Latent space로 data가 옮겨지는 과정에서 결과적으로 feature extraction, dim. reduction을 수행하게 된다. why? output과 input 사이의 error를 minimize하도록 학습하는 과정에서 자연스럽게 달성될 것!
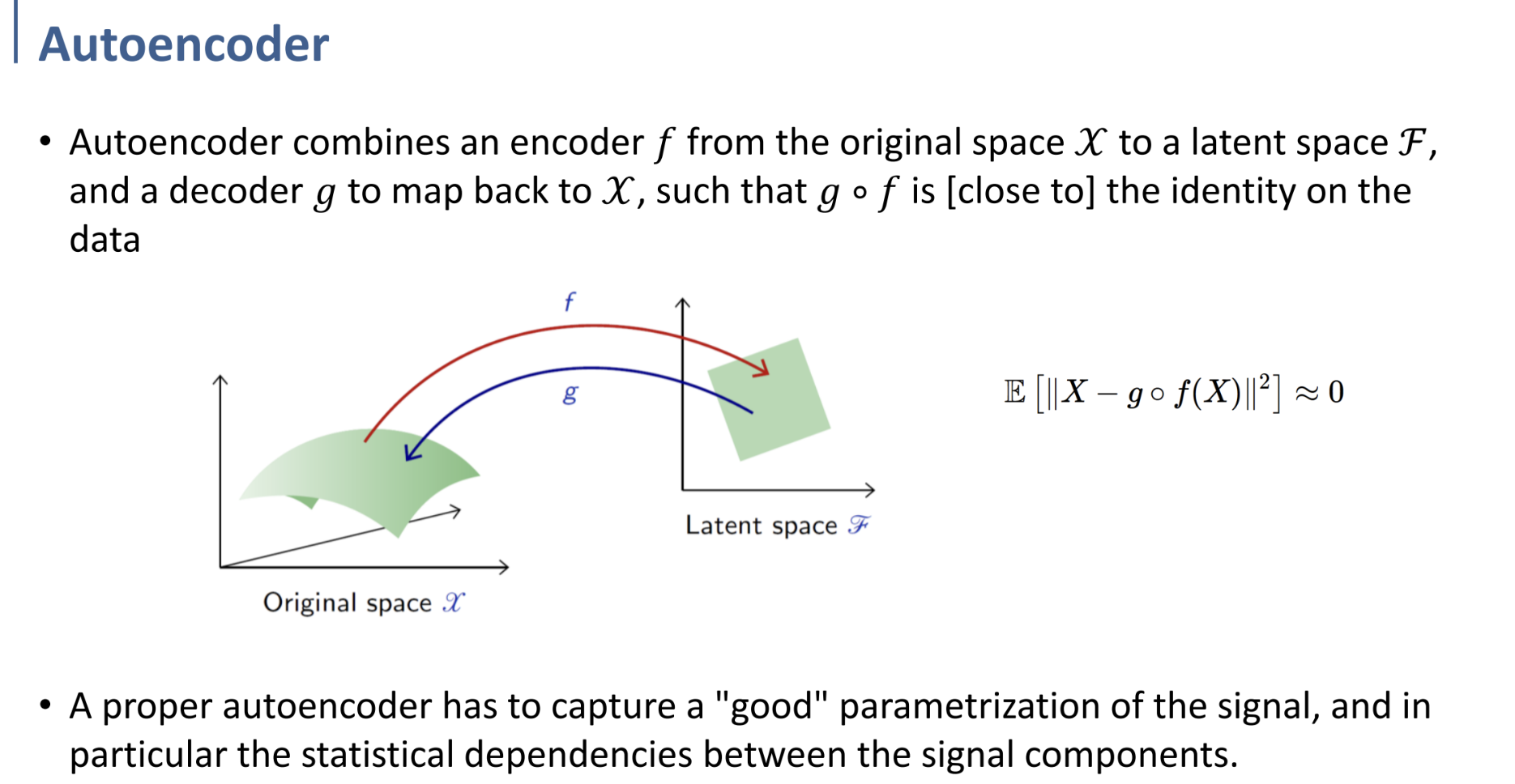
앞에서 설명한 내용과 같은 내용을 시각적으로 표현한 것이다. (3D→2D)
이미 설명한 내용이고, PDF만 보아도 어렵지 않게 이해할 수 있을 것.
$\mathbb{E}[||X-g\circ f(X)||^2]\approx0$
위 식의 뜻 또한 어렵지 않게 이해할 수 있을 것이다.
원본 input과, autoencoder(encoder $f$, decoder $g$)를 거친 output의 2nd norm error가 0에 가깝도록 한다는 것. (물론 2nd norm error인지, 어떤 error인지는 따로 결정할 일.)
autoencoder가 제대로 학습되었다면, dim. reduction 과정에서 “good” feature를 잘 뽑아낼 수 있을 것이고, 그러한 feature들은 서로 최대한 independent한 관계일 것. (PCA를 상기하자.)
Autoencoder as Generative Model
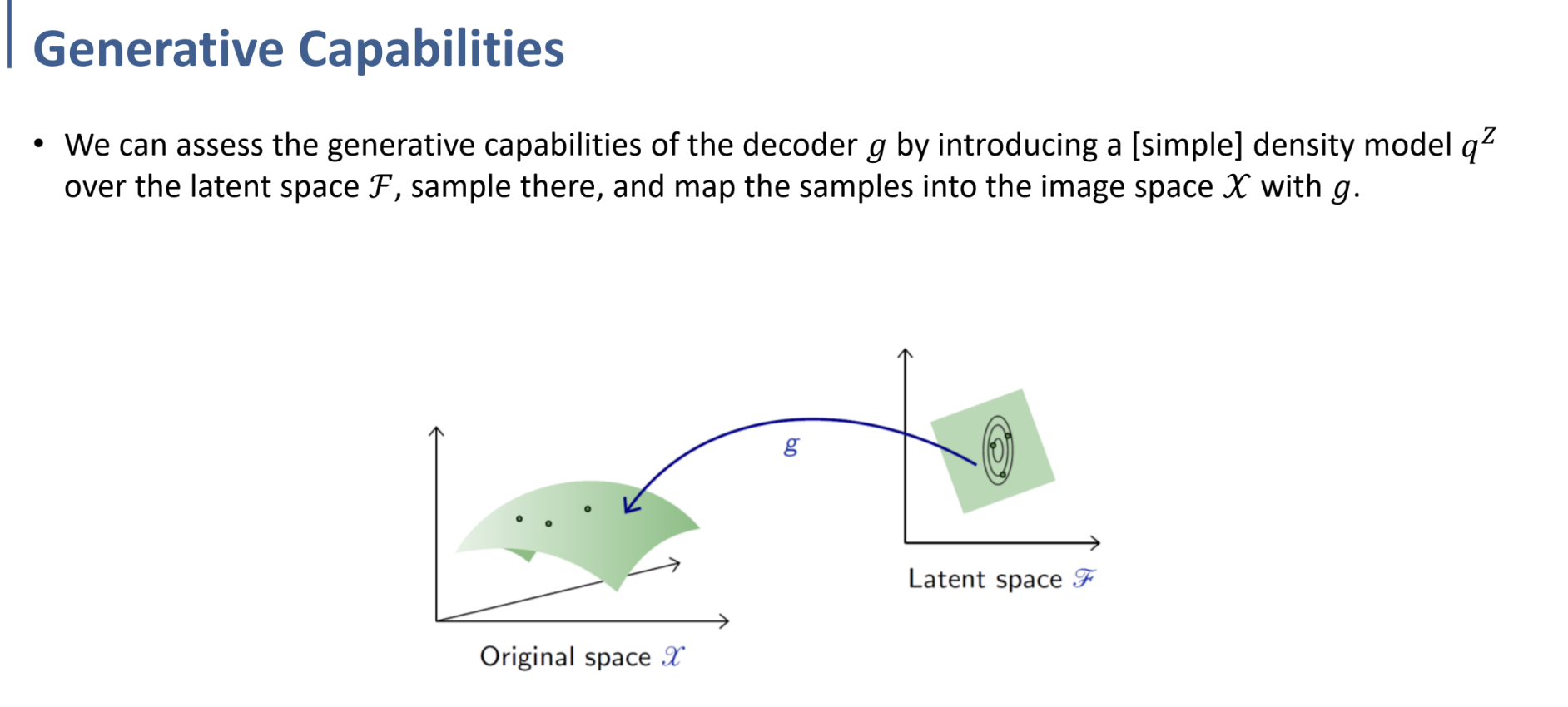
Autoencoder에서 encoder를 제외한 decoder만을 놓고 보았을 때, Latent space에 input을 넣고 forward propagation을 수행하면 Original space의 값이 생성되는 것을 보아 - decoder 자체를 Generative Model로 간주할 수 있다. (Generative model? → 데이터의 분포를 이용해 모델을 학습하여 새로운 sample 생성.)
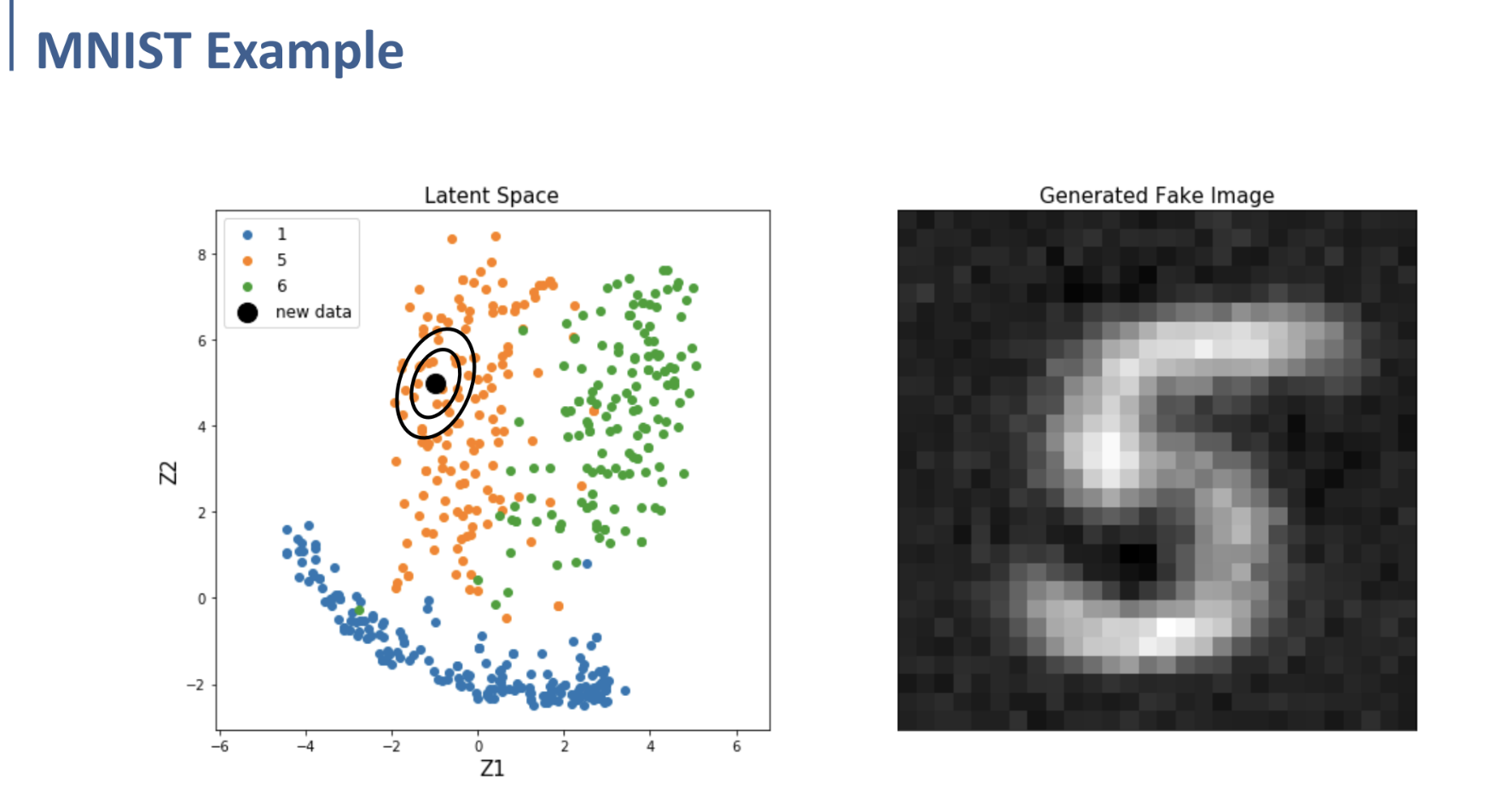
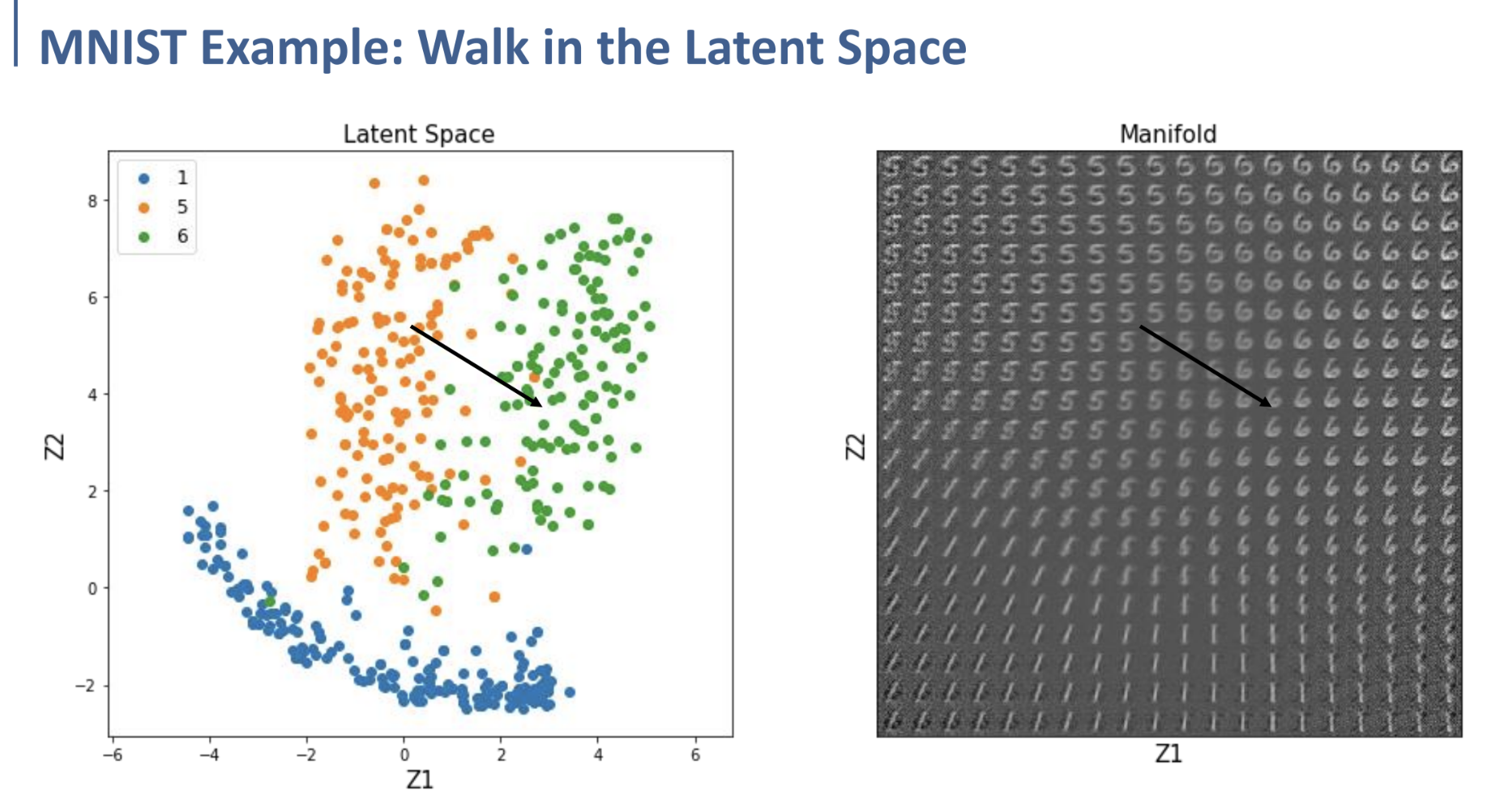
왼쪽은 MNIST dataset으로 학습한 Autoencoder에서, label (1, 5, 6)의 data에 대한 encoding 후의 Latent space에서의 분포이다.
저렇게 label 5에 대한 cluster 쪽에서 Latent Space에 대한 임의의 새로운 data point를 생성하여 decoding시켰을 때, 오른쪽과 같이 새로운 (5로 간주될 수 있는) sample을 생성해낼 수 있다는 것.

잘 학습된 Autoencoder라면, Latent Space에서의 data는 redundancy가 낮고, 최대한 independent한 feature의 axis로 이루어져 있는 구조일 것이다.
이러한 latent space에서의 representation에 대해 직관적으로 이해할 수 있는 예시를 다음부터 설명할 것이다.
우선, 좌측 Original space에서의 그림과 같이, $x, x'$를 random하게 선택한 후, 두 data point를 interpolate(선형보간)하는 것을 상상해 보자.
그러한 interpolate를 수행할 때, Original Space에서 interpolate를 수행하는 것보다, Latent space에서 interpolate를 수행하는 것이 더 make sence하다. (여기까지는 직관적으로 왜 그런 것인지 이해가 잘 가지 않을 수 있으나, 다음의 설명을 확인하자.)
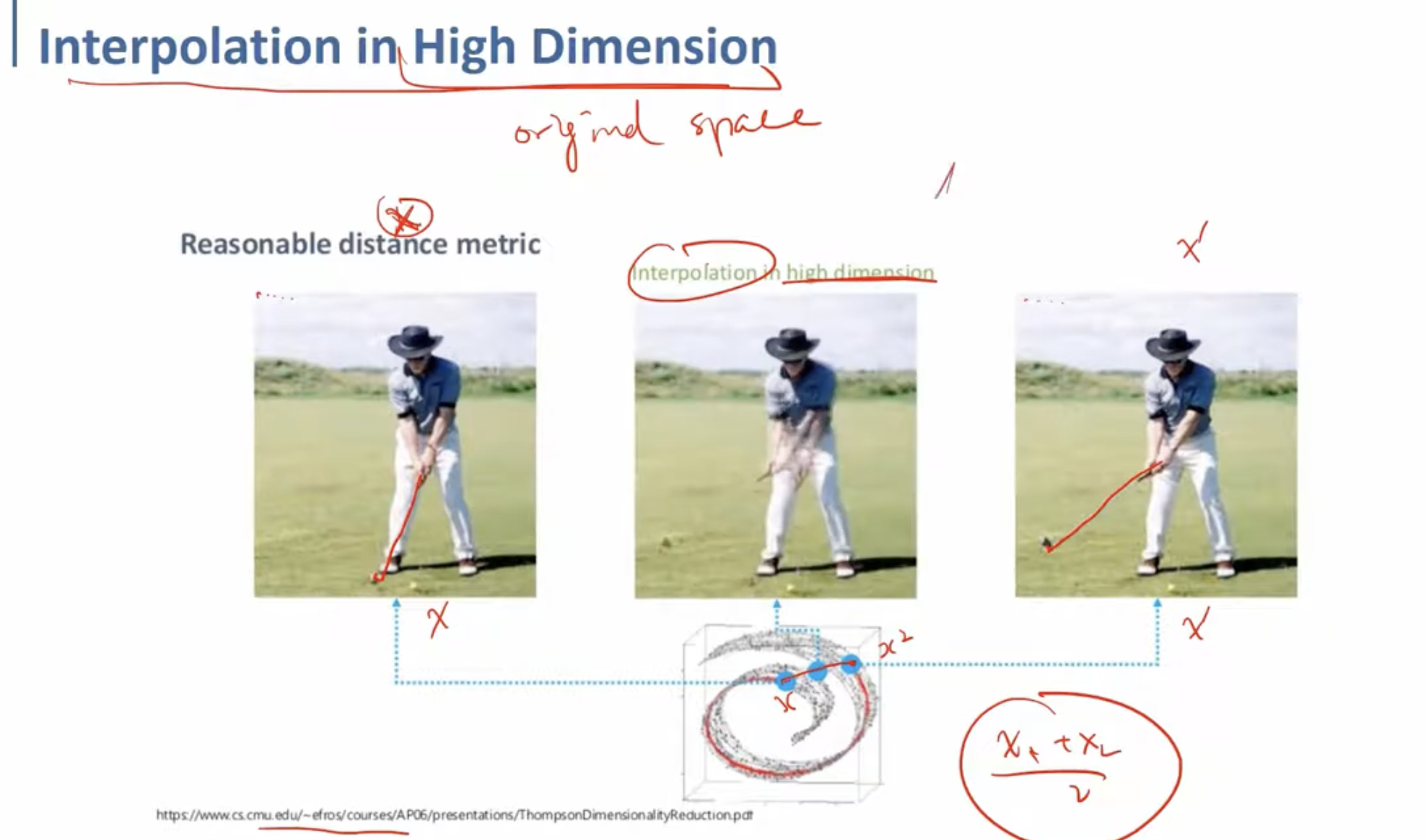
위는 고차원(Original Space)에서 interpolation을 수행했을 때의 예시이다.
골프채를 들고 스윙하는 도중의 사람인데, 왼쪽의 사진과 오른쪽의 사진을 단순히 5:5로 선형보간 하게 된다면, 가운데와 같은 사진이 도출될 것이다.
골프채를 휘두르기 전과 후의 사진이 겹쳐, 움직인 부분이 희미하게 둘 다 나타나 있는 것을 볼 수 있다. 단순히 고차원에서 선형보간을 수행했기 때문에, 그저 픽셀이 원본의 반절 정도의 opacity를 가지고 섞여 표현되는 것이다.
그러나 우리는 직관적으로, 왼쪽과 오른쪽 사진의 특징들을 보간한다면 왼쪽과 오른쪽 사진의 골프채 각도의 정가운데 정도에 골프채가 오는 것이 더욱 바람직하다는 것을 알 수 있다.
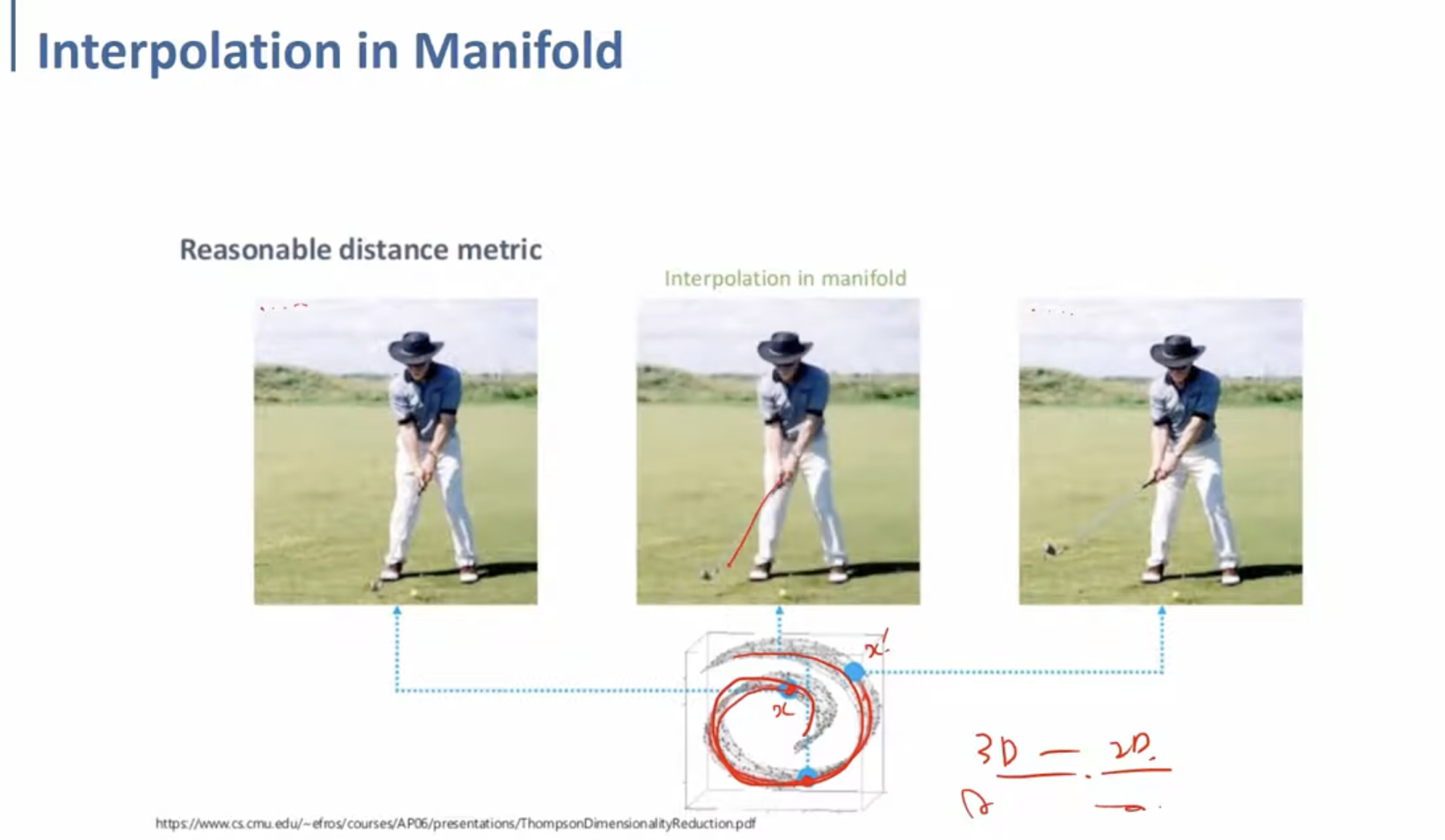
반면 위는 Latent Space에서 interpolation을 수행했을 때의 결과이다.
가운데 사진을 보면, 왼쪽과 오른쪽의 골프채 사이 각도에 골프채가 위치한 것을 확인할 수 있다.
이처럼 Latent space상에서 interpolate하는 것이, 우리가 인지하고 있는 물리적인 보간에 더 가깝게 결과를 도출해낼 수 있다는 것이다. (아래는 MNIST dataset으로 학습한 Autoencoder의 latent space를 visualizing한 예시이다. 오른쪽의 이미지를 보면 1, 5, 6 label에 대한 사진들이 자연스럽게 변화하는 것을 확인할 수 있다.)

Autoencoder로 학습한 decoder를 Generative model로써 사용하는 것은, Latent space가 굉장히 simple하고 inadequate하기 때문에 조금 만족스럽지 않을 수 있다.
→ 그렇기 때문에 더 나은 모델의 필요성을 느꼈고, VAE, GAN과 같은 모델들이 고안되었다.