Reference
https://iai.postech.ac.kr/teaching/machine-learning
https://iai.postech.ac.kr/teaching/deep-learning
위 링크의 강의 내용에 기반하여 중요하거나 이해가 어려웠던 부분들을 정리하여 작성하였고,
모든 강의 슬라이드의 인용은 저작권자의 허가를 받았습니다.
또한, 모든 내용은 아래 Notion에서 더 편하게 확인하실 수 있습니다.
>>노션 링크<<
Keywords
- GAN - Loss Function (MinMax Problem)
- Non-Saturating GAN Loss
- Conditional GAN
Non-Saturating GAN Loss

Generator의 objective function인 $\underset{G}{min} \ E_{z \sim p_z(z)} [\log (1 - D(G(z)))]$ 을 통해 Generator를 training할 때 발생하는 문제가 있다.
$y=log(1-x)$의 그래프를 그려 보면, 오른쪽과 같은 것을 볼 수 있는데, 이를 통해 $D(G(z))=0$ 일 때의 gradient가 작은 것을 확인할 수 있다.
이 때문에 학습 초반, Discriminator에 비해 Generator의 학습이 느려지는 효과를 야기한다.

이를 해결하기 위해, Generator의 Objective function을
$\underset{G}{min} \ E_{z \sim p_z(z)} [\log (1 - D(G(z)))]$ 대신 $\underset{G}{max} \ E_{z \sim p_z(z)} [\log D(G(z))]$ 를 이용하자는 아이디어가 나왔다.
최적화의 관점에서는 결국 동일한 문제를 푸는 것이지만,
우측에서 $y=log(x)$의 그래프를 보면 알 수 있듯, $D(G(z))=0$ ($x=0$)에서의 gradient가 높기 때문에 원활한 학습이 이루어질 것을 기대할 수 있다.
$\underset{G}{max} \ E_{z \sim p_z(z)} [\log D(G(z))]$ 는 원래 Generator에 대한 objective function이 $min$이였기 때문에,
$\underset{G}{min} \ E_{z \sim p_z(z)} [-\log D(G(z))]$ 로 바꾸어 사용하는 것으로.

그래서 결국 최종적으로 정의된 Objective Function인 MinMax Problem은 위와 같이 정리된다.
Conditional GAN

앞에서까지 학습하였던 GAN에서의 Generator는, fake image를 Discriminator가 real image라고 인식하도록 하는 것만을 목표로 하였다.
어떤 fake image를 generate하는 것인지에 대해서는 전혀 관심을 두지 않았다는 것이다.
MNIST dataset이라고 예를 들어 보자. 원래의 GAN의 Generator라면, 어떤 가우시안 분포 Latent Code에서 일정 부분 noise를 섞어 generate하고, 그 이미지를 Discriminator가 fake image라고 인식하는 것에만 집중하였지, 1~9 중 어느 숫자에 대한 이미지를 만들어낼 것인가에 대한 고려는 전혀 하지 않았다.
Conditional GAN (CGAN)에서는,
기존의 GAN처럼 알 수 없는 noise distribution에서 무작위로 sample을 만들어내는 것이 아니라,
Generator가 특정한 조건이나 특성을 가진 fake sample을 만들어내는 것을 학습한다.
(말하자면, 위에서 말한 것처럼 특정한 label이나 class에 대한 이미지를 만들도록 한다는 것이다.)

(MNIST dataset으로 예시를 든 경우이다. 왼쪽의 one-hot encoding된 condition을 추가로 넣어주면, 오른쪽과 같이 그 condition에 맞는 fake sample을 GAN이 생성하도록 학습한다는 것.)

그렇다면, 그러한 CGAN (Conditional GAN)은 어떻게 구현이 되는지 살펴보자.
원래의 GAN의 구조와 크게 달라지지 않는다.
다만 오른쪽 그림과 같이 기존의 구조에서 Generator와 Discriminator에 Class 정보가 들어가며, (Generator는 어떤 class의 fake sample을 generate해야 하는 지, Discriminator는 이 sample이 어떤 class에 해당하는 지 알아야 하기 때문.)
real data를 sampling할 때에도 class 정보를 넣어준다. (그 class에 맞는 real data만 뽑아내어 학습에 사용해야 하기 때문이다.)
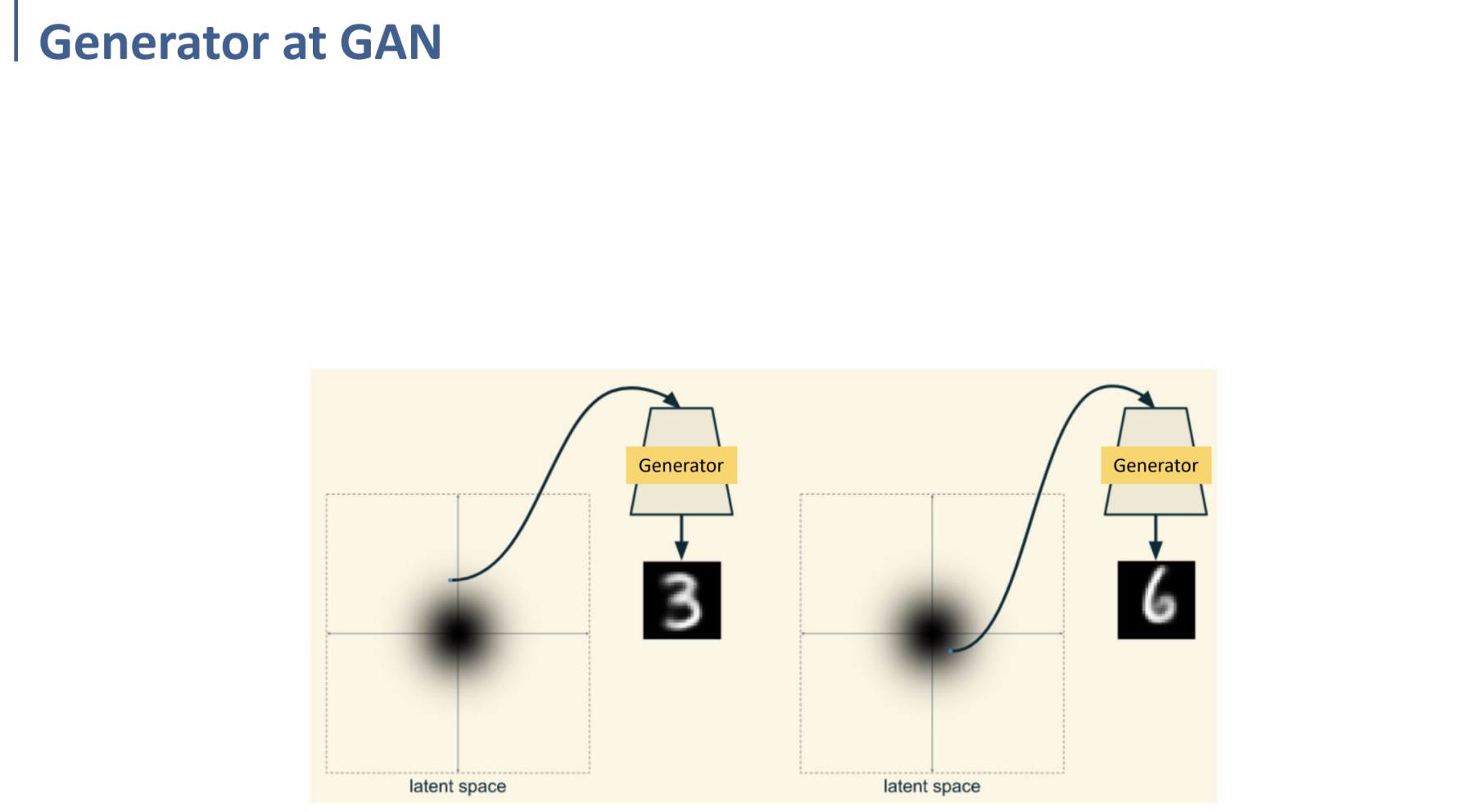
그림이 2차원에 normal distribution(또는 gaussian distribution)을 표현한 그림이라고 생각해 보자.
(MNIST의 예시로 생각하였을 때,)
일반적인 GAN으로 학습되었다면, 위와 같이 Latent Space의 어느 특정한 점을 sampling하면, 그 점에서는 3에 해당하는 fake image가 generate되고, 다른 점에 대해 sampling하여 generator를 거치면 다른 class에 해당하는 fake image가 generate될 것이다.
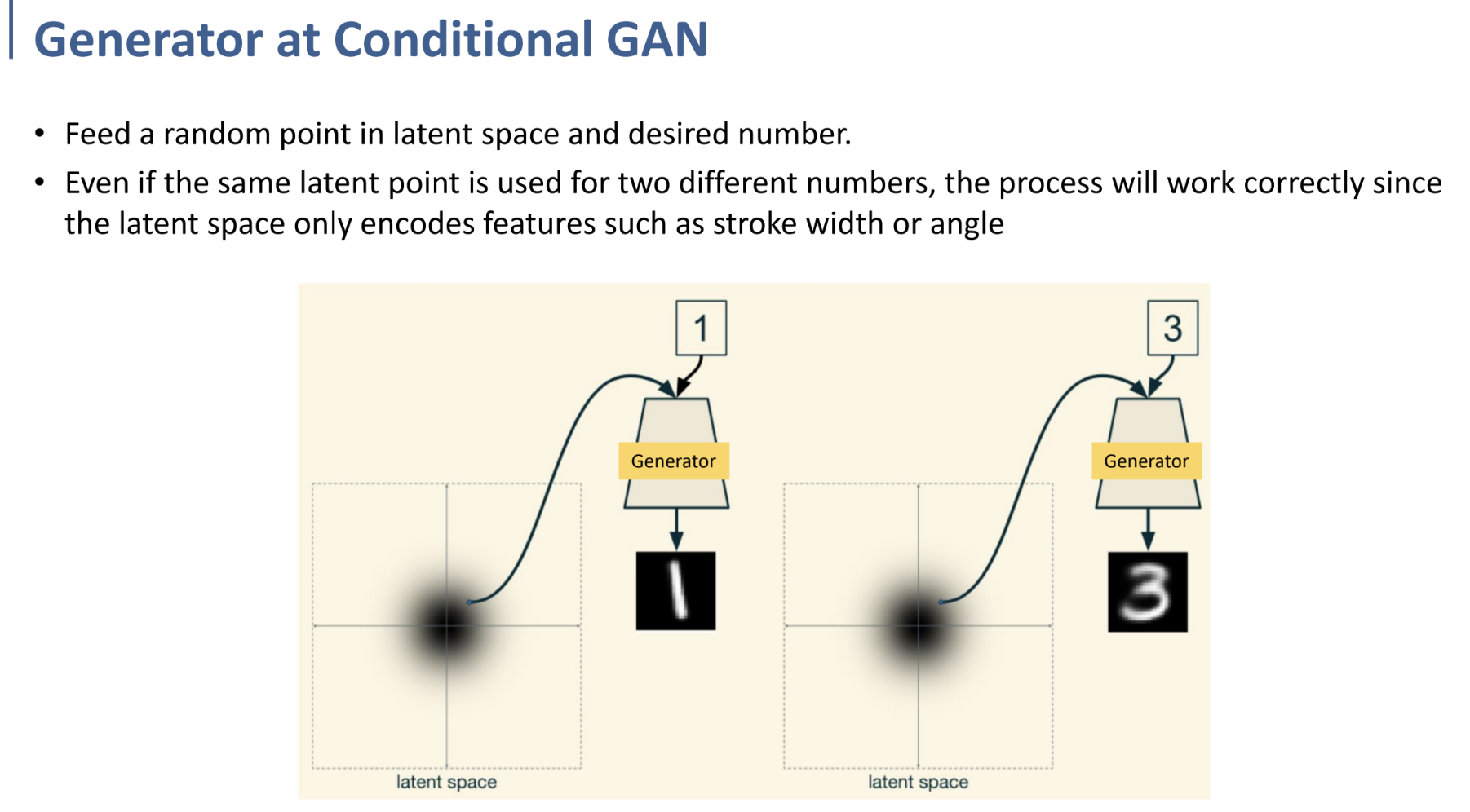
그러나 CGAN에서는 generator를 거칠 때 class 정보를 같이 포함해주기 때문에, 어떤 랜덤한 점을 sampling하여 generator에 넣든지간에, 우리가 원하는 class의 fake image가 도출된다.
만약 Latent Space상의 같은 point에 대해 generate하더라도, condition을 다르게 걸면 다른 fake sample이 생성되는 것이다.
여기에서, Latent Space는 오직 stroke, angle과 같은 특정한 feature들을 Latent Space상의 위치에서 나타내게 될 것(encode)이다. class는 고정된 상태로!
*Conditional GAN 논문 참조