Reference
https://iai.postech.ac.kr/teaching/machine-learning
https://iai.postech.ac.kr/teaching/deep-learning
위 링크의 강의 내용에 기반하여 중요하거나 이해가 어려웠던 부분들을 정리하여 작성하였고,
모든 강의 슬라이드의 인용은 저작권자의 허가를 받았습니다.
또한, 모든 내용은 아래 Notion에서 더 편하게 확인하실 수 있습니다.
>>노션 링크<<
Keywords
- Convolution (1D, 2D)
- Kernel
- Image
Convolution

Convolution이란?
두 signal(신호)중 한 신호를 reverse(뒤집고), shift(이동)시킨 후, 그 둘의 product(곱)을 Summation(or Integrate)하는 것이다.
signal의 값이 discrete(불연속적)할 때는 sum, signal의 값이 continuous(연속적)할 때는 integral.
signal을 뒤집지 않고, 그대로 shifting한 후 계산한 것을 Cross correlation,
뒤집은 후 shifting하여 계산한 것을 Convolution이라 한다.
1D에서는 Cross correlation과 Convolution 사이에 차이가 있다. (위 pdf의 오른쪽 예시를 보자. 3번째 그래프가 Cross correlation, 4번째 그래프가 Convolution이다.)
그러나 2D에서는 둘의 차이가 없다는 것을 알아두자. 이는 추후 확인할 것이다.
위 PDF의 왼쪽 식은 오른쪽 그래프를 보면, 어렵지 않게 이해할 수 있을 것이다.
여기에서
는 convolution 기호.
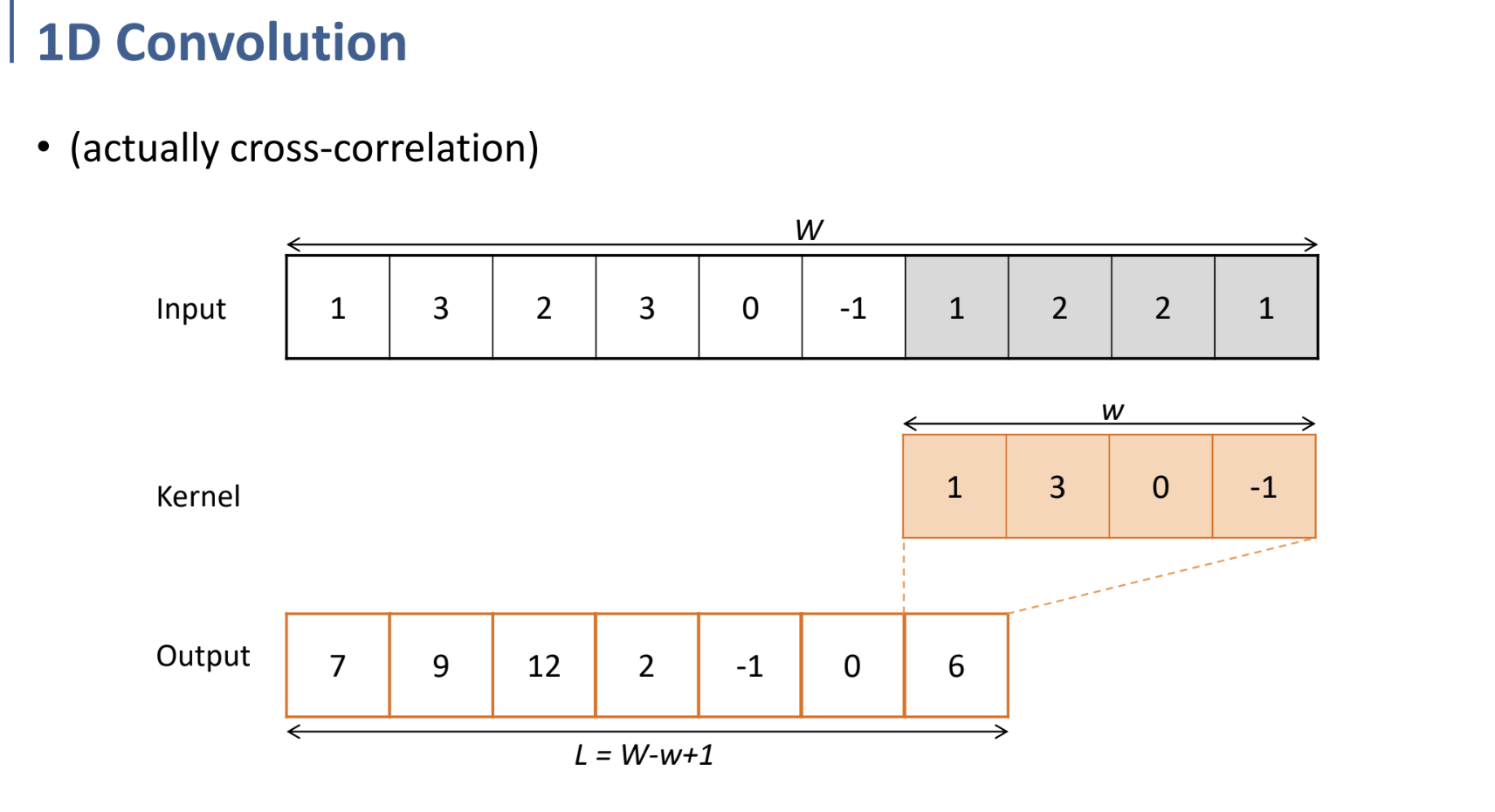
(이 예시는 convolution이 아닌 cross correlation의 예시이나, 뒤집는 것을 제외하고는 동일하기 때문에 그대로 사용하겠음.)
위와 같이 kernel(mask)가 왼쪽에서부터 쭉 shifting(이동)되면서 각각 매칭되는 블럭과 곱하고, 더한 결과를 아래 output에 담기는 것을 어렵지 않게 생각할 수 있다.
이런 식으로 진행되는 것이 1D에서의 convolution.
(output의 길이) = (Input의 길이) - (kernel의 길이) + 1
인 것을 확인하고 넘어가자.
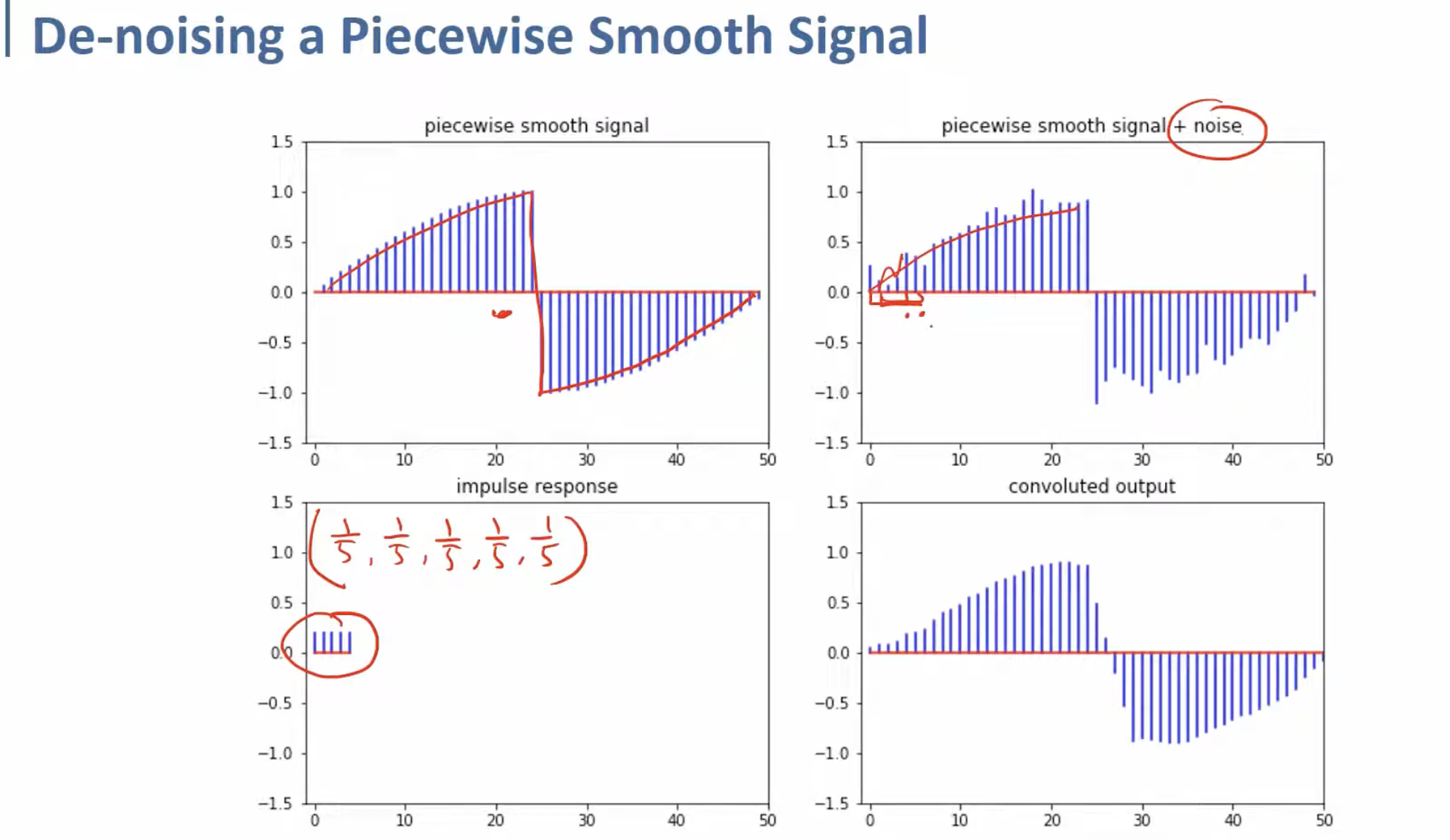
이것은 noise가 들어간 signal을, (
2번째 그래프의 noise가 섞인 signal이, 3번째 그래프의 kernel로 convolution을 수행하면 4번째 그림처럼 smoothing되는 것을 확인할 수 있다.
(뜬금없는 예시이지만, 다음 설명을 위한 것이다.)
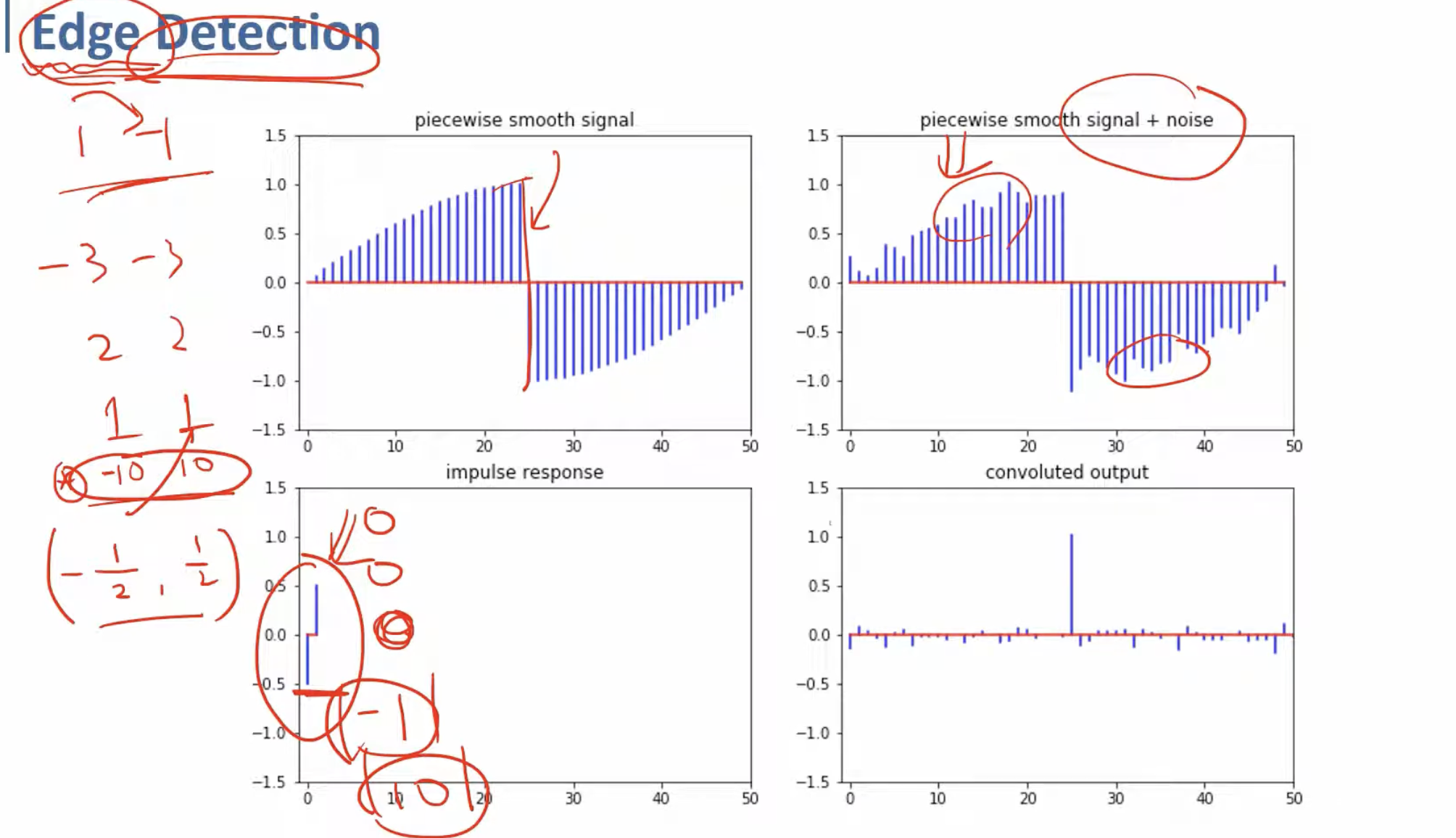
여기서는 똑같은 noise가 포함된 signal을, 3번째 그래프처럼
convolution된 결과 그래프를 보면, 원본 signal의 + → - 로 확 바뀌는 부분을 잘 캐치해낸 것을 확인할 수 있다.
앞의 예시와 함께, 여기에서 우리는 kernel을 어떻게 구성하는지에 따라 여러 역할을 수행해낼 수 있다는 것을 인지해야 한다.
앞의 예시에서와 같은 kernel을 사용하면 signal의 noise를 줄이고, smoothing하는 결과를 낼 수 있으며,
뒤의 예시에서와 같은 kernel을 사용하면 signal이 급격하게 변하는 edge 부분을 캐치(detection)하는 결과를 낼 수 있다.
또 다른 어떤 kernel을 구성한다면, 그 kernel로 convolution한 결과 또한 다른 특정한 부분을 잡아내거나, 어떤 효과를 낼 수 있다는 것이다.

2D convolution에 대해 알아보기 이전에, image는 컴퓨터의 입장에서 matrix로 취급된다는 것을 이해하자.
(색상이 있는 Image의 경우, → RGB 각각에 대한 3개의 matrix / 또는 grayscale된 image를 하나의 matrix로)
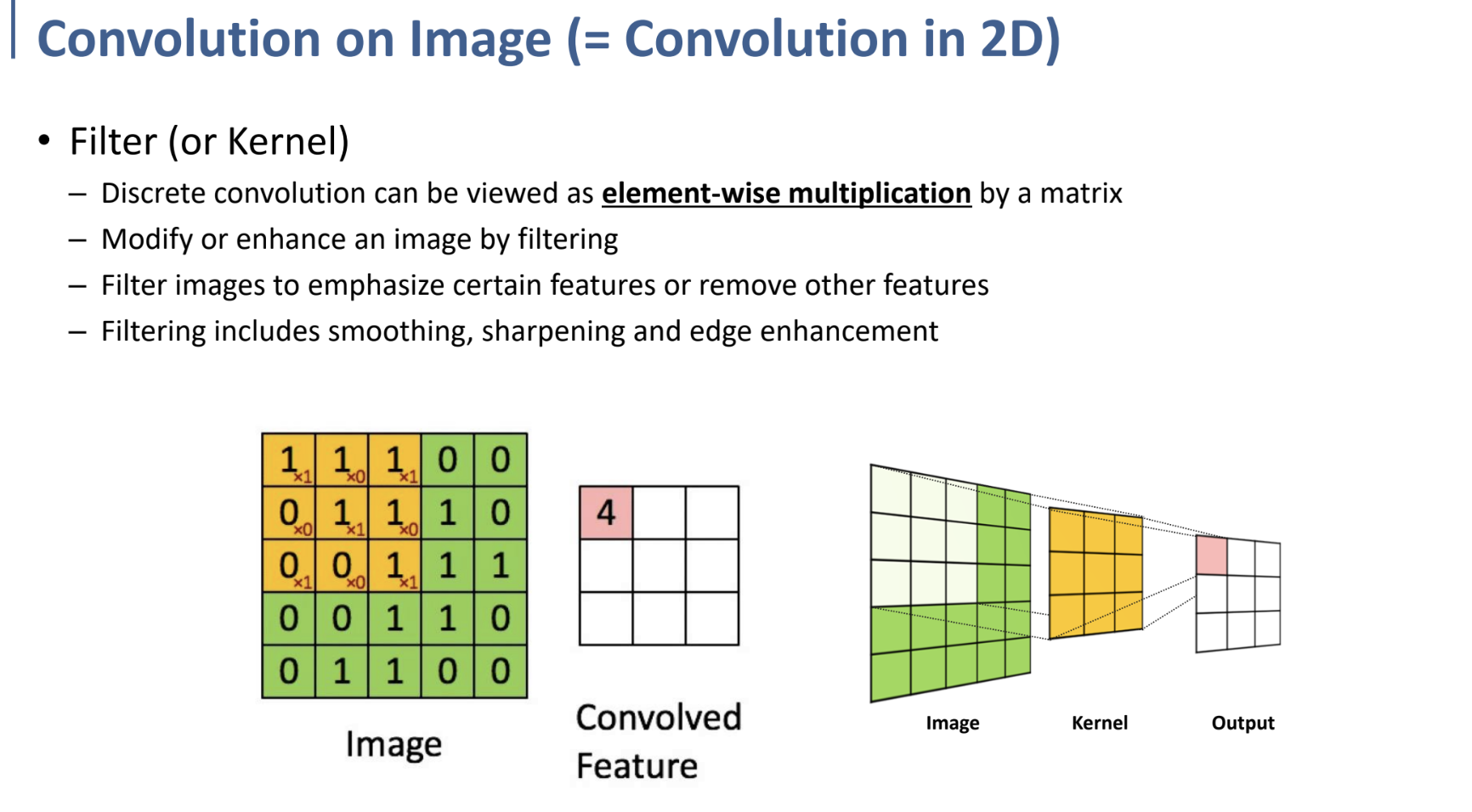
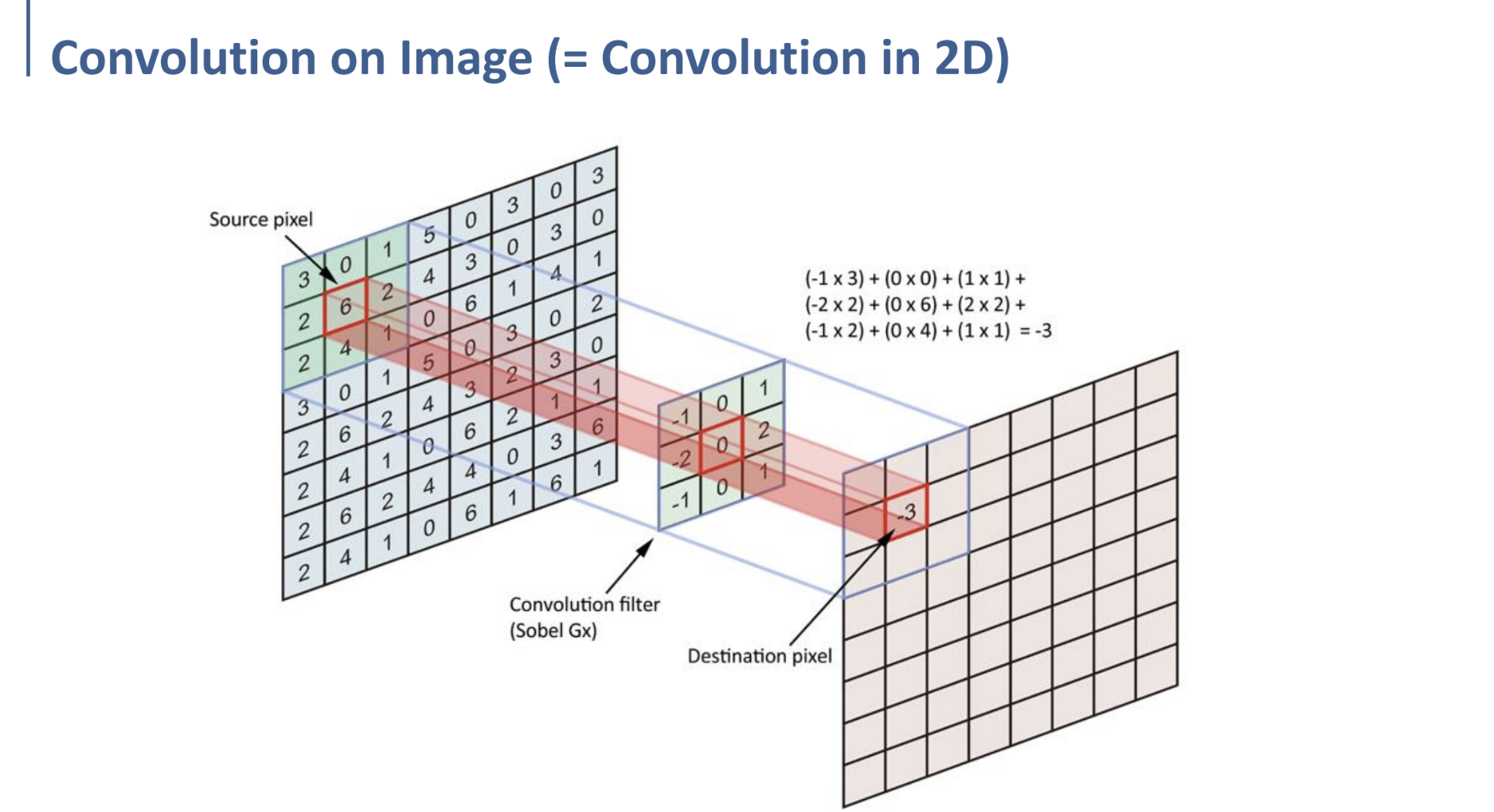
2D convolution은 1D convolution에서의 과정과 개념적으로 크게 다르지 않다.
Filter(kernel)을 이용해 원본 2d matrix(예를 들어, image)에 kernel(filter)를 shifting(이동)시키며 element-wise multiplication(원소별 곱셈)의 합을 계산하는 것이다. (그림 참고)
마찬가지로 이러한 2D convolution을 통해, 이미지의 특정 feature를 강조 또는 제거하거나, smoothing, sharpening.. 등의 작업을 kernel을 다르게 디자인함으로써 수행할 수 있다.

예를 들어 위쪽의 kernel을 이용하면, col 1의
마찬가지로 아래쪽의 kernel을 통해 row 1, row 3의

여기까지 우리는 여러 다른 종류의 Kernel을 통해 image에 특정한 효과를 낼 수 있다는 것을 학습하였다. (앞에서 나온 edge detection 뿐만 아니라, blurring, noising, … 또는 어떤 원하는 정보를 얻어낼 수 있는 무엇이든.)
이제 이 과정을 반대로 생각해 보자. 우리가 어떤 정보를 얻기 위해 원하는 kernel을 구성하는 것이 아니라,
data로부터 kernel을 학습하도록 하게 될 것이다. (Supervised Learning)
Deep Learning을 통해 특정 feature를 extract하는 kernel을 학습하고, 그 구조를 만들어 내는 것이 우리의 목표!