Reference
https://iai.postech.ac.kr/teaching/machine-learning
https://iai.postech.ac.kr/teaching/deep-learning
위 링크의 강의 내용에 기반하여 중요하거나 이해가 어려웠던 부분들을 정리하여 작성하였고,
모든 강의 슬라이드의 인용은 저작권자의 허가를 받았습니다.
또한, 모든 내용은 아래 Notion에서 더 편하게 확인하실 수 있습니다.
>>노션 링크<<
Keywords
- Time Series Data
- Markov Chain (Markov Process)
- Hidden Markov Model (HMM)
- Kalman Filter
Markov Process (Markov Chain)

- 이전까지 학습한 대부분의 Classifier(모델)들은, data의 sequential한 부분, 즉 시계열 데이터에 대한 고려를 하지 않았다. 앞으로는 그러한 데이터에 대해 다루어 보자.
- System이 N개의 discrete한 state 중 하나의 상태를 가질 수 있다고 생각해 보자.
- 예를 들어, $q_t \in {S_1, S_2, ..., S_n}$ 이면, time index $t$ 마다 각각 $S_1, …$의 상태 중 하나를 갖는다는 것이다.
$p(q_0, q_1, \cdots, q_T) = p(q_0) p(q_1 \mid q_0) p(q_2 \mid q_1 q_0) p(q_3 \mid q_2 q_1 q_0) \cdots$
전체 Time series data sequence에서, $q_0, q_1, …, q_T$ 에 각각 특정 state일 전체 joint probability는,
$p(q_0) p(q_1 \mid q_0) p(q_2 \mid q_1 q_0) p(q_3 \mid q_2 q_1 q_0) \cdots$ 와 같이 표현될 수 있다.
$t=0$ 에서 특정 state일 확률 $p(q_0)$.
그 이후 $t=1$ 에서 특정 state일 확률. conditional probability인 $p(q_1|q_0)$
… (이후 반복)
그러나 이렇게 표현하면 수학적으로는 맞지만, 현실적으로 계산할 수 없게 된다.
그렇기 때문에 사용하는 것이 Markov Chain.

Markovian property 라는 성질을 이용하게 된다.
이 성질이 의미하는 것은, 과거에 어떤 state를 거쳐왔든지간에, 현재 state에서 다음 state로 갈 확률은 항상 동일하다는 가정을 깔고 간다는 것이다.
다시 말해, 현재 시간 $t$ 에서의 상태가 $q_t$라면, $t+1$ 시간의 상태 $q_{t+1}$로 전이될 확률은, 시간 $0 \sim t-1$ 에서의 상태와는 전혀 관계없이 항상 동일하다는 것이다.
이러한 가정은, $0 \sim t-1$ 시간까지의 정보를 $t$ 시간의 상태가 가지고 있다는 전제를 두고 이루어질 수 있다.
이렇게 Markovian property를 가져 현재의 state가 바로 이전 state에만 영향을 받으며, time interval이 discrete한 probability process (sequential process)가 Markov Process인 것이다.
물론, 엄밀하게 말하자면 모든 Time Series data에 markov process를 적용하여 계산할 수 있는 것은 아니다. 다만 시계열 데이터를 분석하고 계산하는 데에 있어 편의를 위해 어느 정도 감안하고 사용하는 것이다.
이러한 Markov property의 가정을 이용하여 Markov Process를 사용하게 되면, 이전 state의 확률을 고려하지 않아도 되기 때문에, 전체 joint probability를 계산할 수 있게 된다.

그래서 그러한 Markov Chain을 이용하여-
어떤 Markov state $s$ 에서 다음 state $s'$ 로 전이될 확률은 다음과 같다.
$P_{ss'} = P[S_{t+1}=s'\ | \ S_t=s]$
그리고 맨 윗 장에서 보았듯이 이러한 discrete한 state가 N개 존재하기 때문에, 모든 N개의 state에서 N개의 state로 전이되는 전이 확률을 모두 모으면 아래와 같이 matrix로 표현할 수 있다.
$P = \text {from}
\overset{\text{to}}{\begin{bmatrix}
\mathcal{P}_{11} & \cdots & \mathcal{P}_{1n} \\
\vdots & \ddots & \vdots \\
\mathcal{P}_{n1} & \cdots & \mathcal{P}_{nn}
\end{bmatrix}}$

종합하자면, Markov Process를 위와 같이 정의할 수 있다.
Markov Process는 memoryless(이전 상태를 신경쓰지 않는다는 뜻)한 random process이고,
passive한 stochastic behavior를 표현한다.
이를 통해 Markov property를 가지는 시계열 데이터 sequence $s_1, s_2,…$가 생길 것.
그리고 아래 박스에 있는 요소들이, Markov Process를 결정짓는 요소들이다.
(Markov Process를 define하는 세 요소들)

위는 예시.
Hidden Markov Models (HMM)

Hidden Markov Model
기존의 Markov Chain에서 변형된 형태로, 위 pdf의 그림에서 X가 전이되는 줄만 떼어 보면 Markov Chain과 동일하다.
그러한 Markov Chain에서의 true state가 unobservable하다고 가정하고, 그 state에만 dependent한 (사진에서는 Y) sensor가 존재하는 형태이다.
true state (원본 상태) 는 우리가 파악할 수 없으며, 그것과 일부적으로 관련된 sensor만 우리가 관찰할 수 있는 상황인 것이다.
예를 들어 보자. 우리가 어제 비가 왔는지, 오지 않았는지 모르는 상태이며, 비가 왔는지를 알고 싶다고 하자.
그리고 우리는 어제의 습도만을 알고 있다고 하자. 습도 정보를 통해 우리는 비가 왔는지를 추론할 수 있다.
이 때 어제 비가 왔는지, 오지 않았는지의 상태가, 관측 불가능한 hidden state(true state)인 것이며,
우리가 알고 있는 습도 정보가 sensor에 해당하는 것이다.
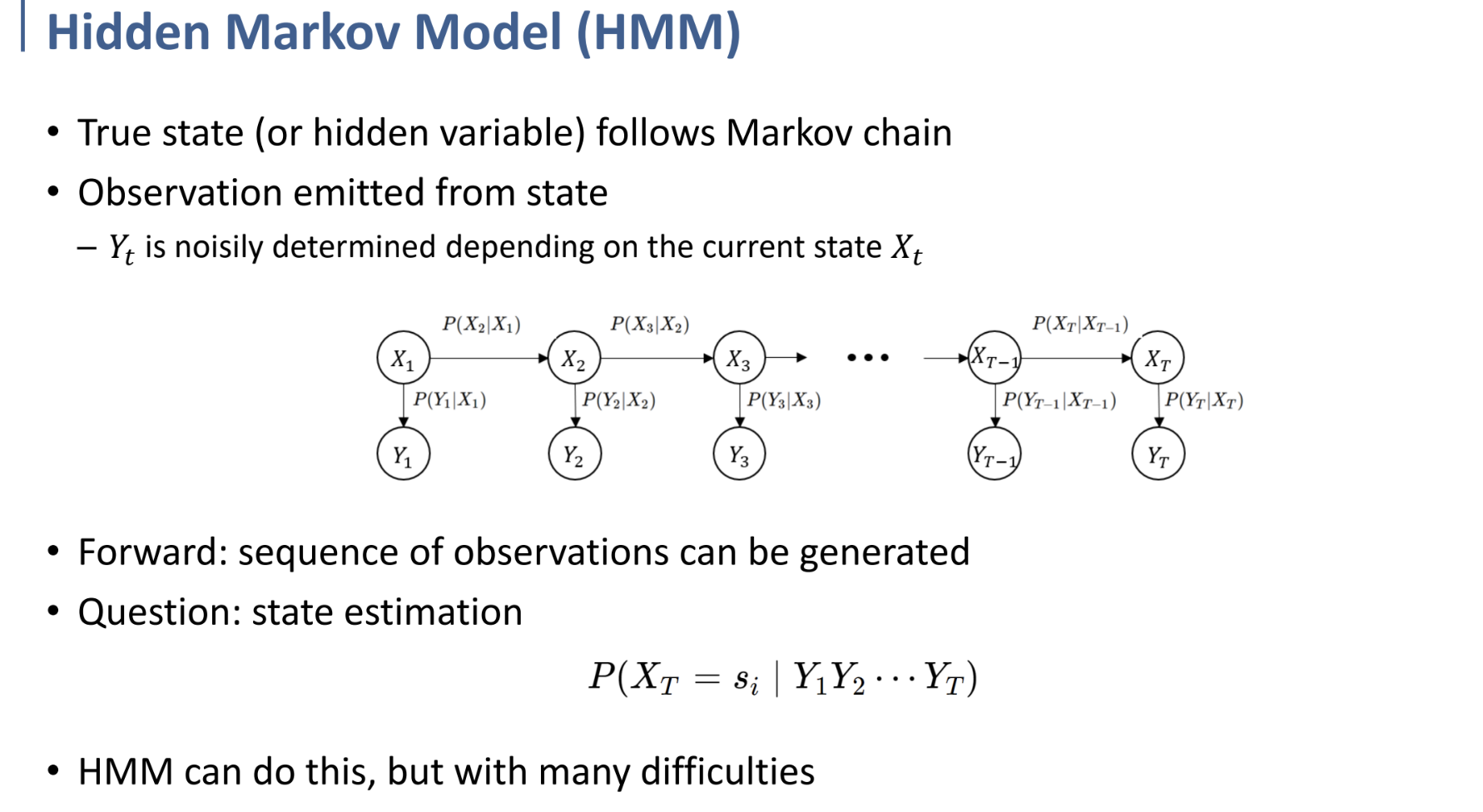
그림에서 위쪽 Chain(True State, Hidden variable)은 Markov chain을 따른다고 하자.
Observation (Y)는 state(X)로부터 emit되는 것이다.
따라서, Y는 현재의 state X에만 dependent하며, noisy한 정보이다.
Markov Chain에서 우리에게 주어졌던 것이 State(X)의 sequence였다면,
HMM에서 주어지는 것은 Observation(Y)의 sequence이다.
이 observation들의 sequence를 이용하여, 현재 시간의 true state를 추론하고 싶은 것이다. (State estimation)
여기에서 HMM에 대한 자세한 것들을 다루기보단, 그저 Time Series Data를 다루던 하나의 Model이라는 것 정도와, 그 구조만 인식하고 넘어가자.
Kalman Filter
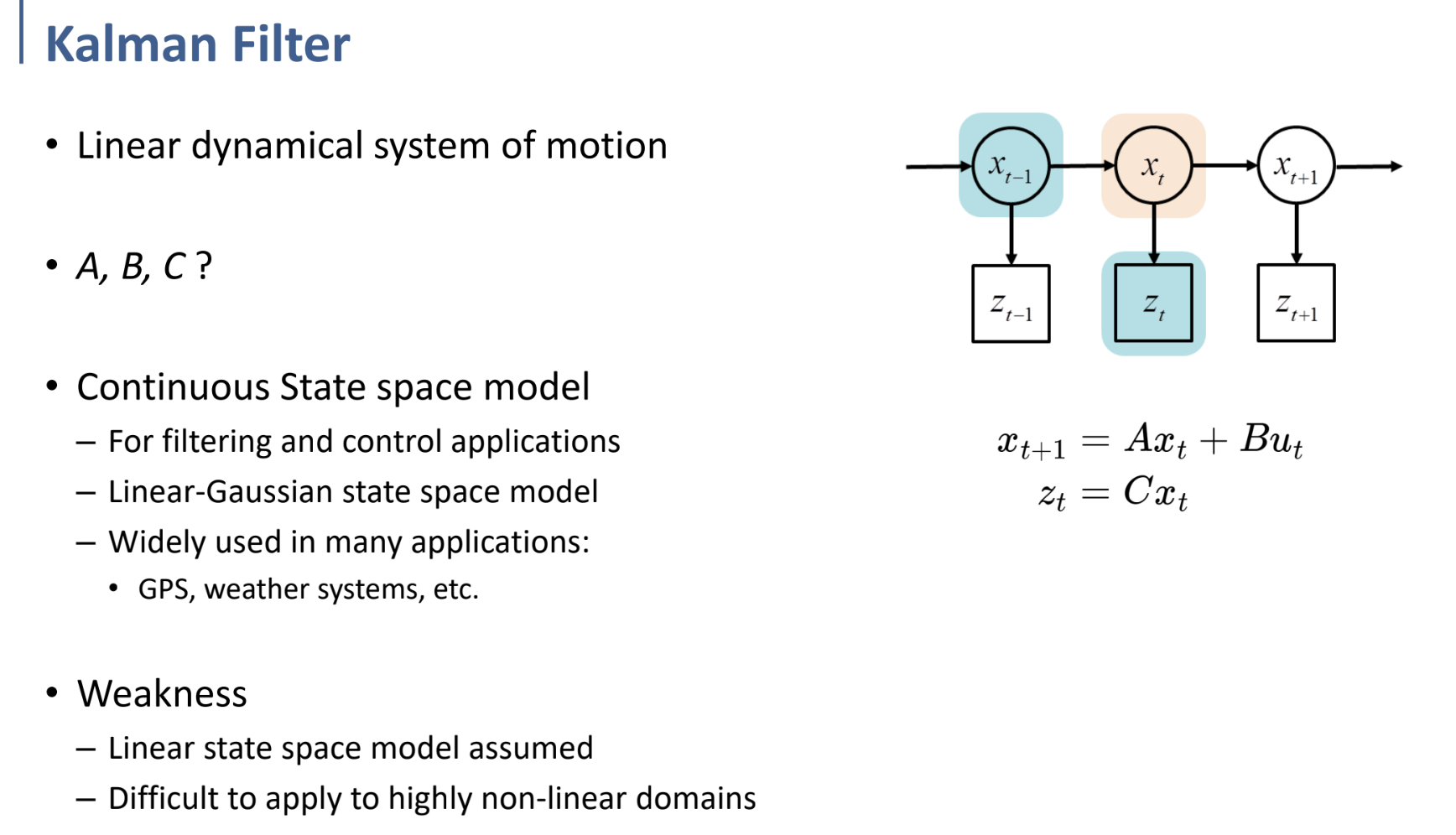
Kalman Filter란.. 간단히 말해서 우측 그림과 같은 Linear dynamical system에서, prediction값과 observation값을 결합해 추정치를 더 정확하게 만드는 알고리즘이다.
$x$를 state, $u$를 input, $z$를 observation값이라 하자.
Linear한 system에서, 우측 식과 같이 다음 state와 observation값을 계산할 수 있다.
$x_{t+1} = Ax_t + Bu_t$ 를 통해 현재 상태에서 다음 상태로의 전이를 모델링하고,
$z_t = Cx_t$ 를 통해 현재 상태에서 관측값을 도출해낼 수 있다.
이 구조와 행렬 A, B, C가 적절하게 구성되어 있다면,
이전 상태 $x_{t-1}$을 통해 현재 상태 $x_t$를 예측하고,
실제 관측값 $z_t$를 통해 예측된 현재 상태를 업데이트시키는 과정을 거치는 것이다.
이러한 Kalman Filter를 사용해 Time Series Data를 처리하는 방식은,
Linear state space model을 미리 구축해야 한다는 점과,
non-linear domain에 대해서는 잘 맞지 않는다는 단점이 존재한다.