Reference
https://iai.postech.ac.kr/teaching/machine-learning
https://iai.postech.ac.kr/teaching/deep-learning
위 링크의 강의 내용에 기반하여 중요하거나 이해가 어려웠던 부분들을 정리하여 작성하였고,
모든 강의 슬라이드의 인용은 저작권자의 허가를 받았습니다.
또한, 모든 내용은 아래 Notion에서 더 편하게 확인하실 수 있습니다.
>>노션 링크<<
Keywords
- RNN
- Recurrence
- Finite Response Model / Infinite Response Model
- State-Space Model
- RNN Training (Backpropagation)
RNN - Recurrence

위와 같은 시계열 데이터(Time Series Data)가 들어왔을 때,
그 원본 데이터 (Measurement, Observation - 여기서는 Y.) 로 Classification이나.. 어떤 predict를 수행할 수도 있을 것이다.
물론 그런 raw한 data로부터 prediction을 수행할 수도 있겠지만, 그러한 observation(Y)보다 더 중요한 정보만을 담고 있는, compress된 information만을 담고 있는 무언가를 도출해낼 수 있겠다- 라는 가정 하에, 다음 이미지와 같이 Network를 update시킬 수 있을 것이다.

위와 같이, 가운데에 Hidden Layer (Latent space, variable)이 생긴 형태의 Network로 바꿀 수 있다.
그렇게 되면, 이제 Observation(Y)가 아닌, hidden state(X) 정보로부터 classification(prediction 등)을 수행하게 될 것이다.
그러나 이 상태의 Network에서는, 각각의 time index마다의 정보가 independent하게 작동한다는 것을 시각적으로도 쉽게 확인할 수 있다.
그렇게 해서는, Time Series Data에서의 가장 큰 특징인, 시간의 흐름 속에서 발생하는 정보들을 잡아낼 수 없고, 이용할 수 없다.

그래서, 그러한 시계열 데이터 속에서의 dynamic behavior를 담기 위해서는 위와 같은 형태로 hidden state(latent state, hidden layer)를 연결해 주어야 한다.
화살표로 각 hidden state를 이어줌으로써, 각 hidden state간의 관련성을 사용할 수 있도록 해놓는 것.
그러한 dynamic behavior들이 state (hidden state. latent state) 속에 담겨 있다는 것이며, 그것을 표현하기 위해 위와 같은 구조를 짜 놓고, 학습을 통해 $\omega$를 갱신하며 시계열 데이터 속의 dynamic한 information을 catch하는 것이 목적이다.
이 과정에서, Kalman Filter이나 HMM에서의 Transition matrix와 같은 것들은 미리 준비되어 있어야 했지만, 우리는 RNN에서 이 상태의 전이를 학습시키겠다는 것. (+ Observation에서 Latent state로도 또한.)

그래서 “Recurrence”에 대해 간단히 정의해 보자면,
$s^t = f(s^{t-1};\theta)$ 처럼, 현재 $t$시간에서의 state를 알기 위해, $t-1$시간에서의 state를 사용하는 것.
이 때, 여기서의 $f$ 와 hidden state representation을 sequential data를 통해 RNN에서 학습하게 될 것이다.

그리고 앞으로, RNN에서 Network의 구조를 위와 같이 사각형의 형태로 간단하게 표시할 것이다.
Input은 시계열 데이터 상에서 각 time index에 해당하는 data이며, (회색 동그라미들)
각 Layer는 각각 neuron들을 가지고 있을 것이다. 이 많은 neuron들을 모두 동그라미로 하나하나 표시하기에는 복잡해지므로, 하나의 Layer를 사각형으로 단순하게 표시할 것.
RNN - Infinite Response Model

여기에서의 회색 사각형은, 앞에서 말했듯 시계열 데이터 상에서 하나의 time index(chunk)에 해당하는 input data이다.
현재 시간에 대한 predict를 하기 위해, 지난 시간 (여기에서는, 현재를 포함하여 4개의 time chunk)들의 정보를 포함하여 predict를 수행한다.
이것은 그냥 CNN 구조를 sequential data에 그대로 적용한 것 뿐이다.
또한 여기서 sliding을 한다는 것은, 아래 그림과 같이 다음 시간에서 predict를 수행할 때도, 일정 개수의 time chunk input만 사용한다는 것.
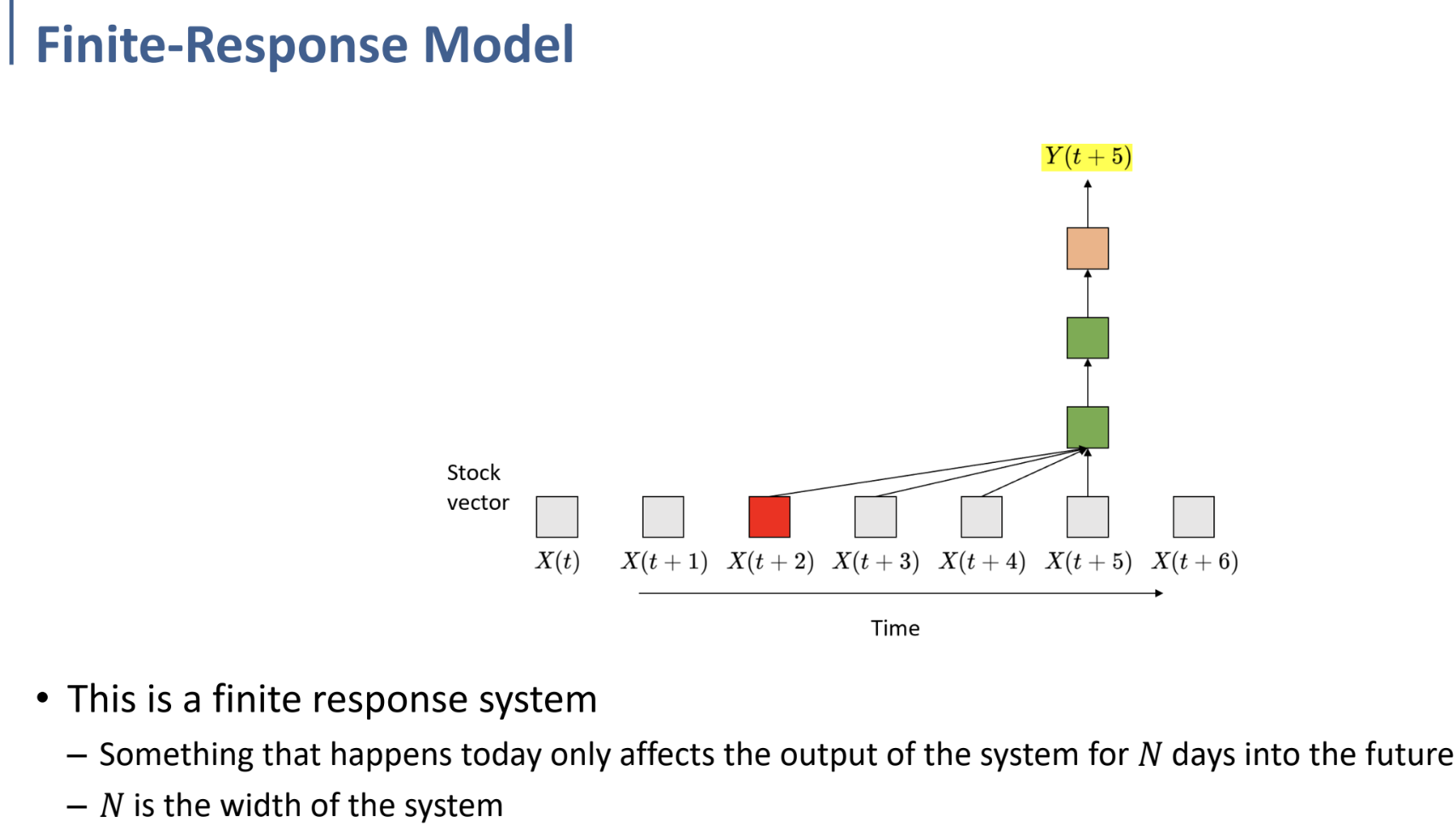
이것을 조금 더 일반화하면, Finite-Response Model이 된다.
- 오늘 일어난 일이, 다음 N 일(N개의 time chunk) 동안의 output에만 영향을 미치게 된다. (Finite하다.)
- N은 우리가 define하게 될, system의 width이다.
이를 수식으로 표현하면 아래와 같다.
$Y_t = f(X_t, X_{t-1}, …, X_{t-N})$
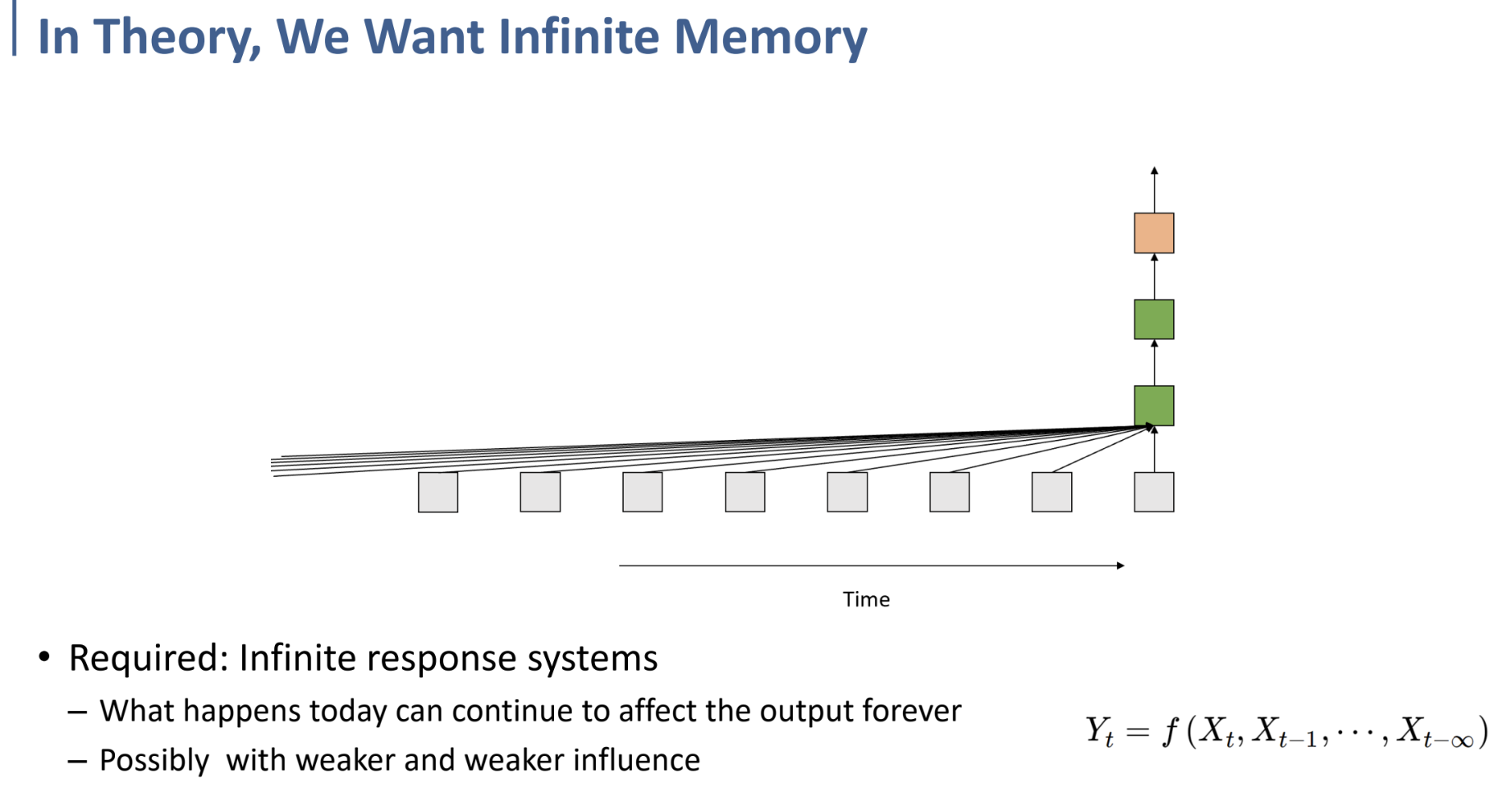
그런데 만약, 우리가 과거의 데이터를 무한정(Infitine) 현재의 output을 도출하는 데에 사용하고 싶다면, 위와 같이 표현될 수 있을 것이다.
- 오늘 일어나는 일이 이후 모든 output을 도출하는 데에 영향을 미치게 되며,
- 그 영향은 갈수록 약해질 것이다. (시간이 멀어질수록 영향이 약해질 것.)
그러나 이렇게 무한한 과거의 데이터를 사용하는 것은, 현실적으로 계산할 수 없게 된다.

그런데 만약 이러한 Infinite Response System을 아래와 같이 표현하면 어떨까?
$Y_t = f(X_t, X_{t-1}, …, X_{t-\infty}) \rightarrow Y_t=f(X_t, Y_{t-1})$
우측과 같이 recurrent, recursive하게 표현한다면, $Y_{t-1}$이 과거의 모든 input에 대한 영향을 함축하고 있을 것이기 때문에, 의미가 변하지 않고 식을 간단히 줄일 수 있다. (물론 계산도 가능해지게 된다.)
Finite한 Network. Infitine한 Response. Nonlinear Autoregressive.
그리고 이러한 output $Y_t$ 는 물론, 과거의 모든 information을 포함하게 될 것이다.

그러한 Autoregressive한 전체적인 Network 구조를 표현해 보면 위와 같다.
결국 여기서 중요하게 파악해야 할 것은, 과거의 output이 현재의 output을 도출하는 데에 사용된다는 것.
RNN - State-Space Model

앞에서까지는 output이 recurrent하게 쓰이는, Infinite Response Model을 학습했다.
그렇지만, Markov Chain을 상기해 보자.
과거의 output이 현재의 output을 도출하는 데에 쓰이는, output이 recurrent한 형태보다는,
state가 recurrent한 형태가 더 make sense할 것이다.
이러한 형태를 위 식에서 확인할 수 있다.
$h$ 는 state이며, 이 state가 recurrent한 구조를 갖게 된다.
이를 위해, $h_0$ 또한 계산해주어야 하기 때문에 $h_{-1}$ 을 처음에 define해주어야 한다.
이 형태 자체가 Recurrent Neural Network이다.
물론 state가 recurrent하기 때문에, State는 과거 전체의 Information을 함축하고 있게 될 것이다.
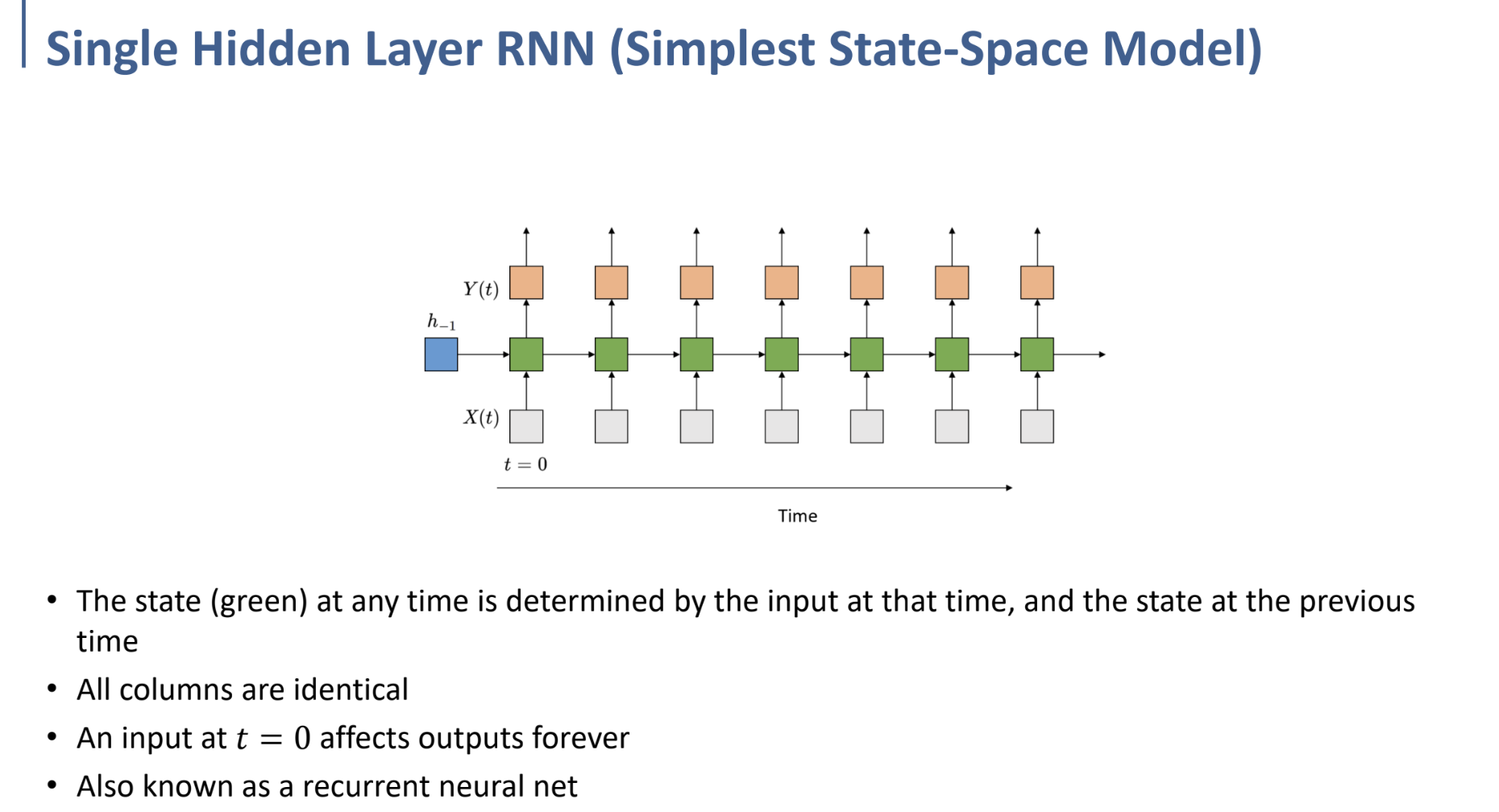
위와 같은 형태가 RNN의 Network이다.
각 시간의 state는 그 시간의 input과 지난 시간의 state로부터 결정되며,
input에 의해 만들어진 state가 recurrent하기 때문에, 현재의 input은 미래의 모든 state에 영향을 미치게 된다.
recurrent layer는 여러 층으로 쌓을 수 있다.

(위는 Recurrent Layer가 2개일 때의 예시이다.)
그래서, 이러한 RNN Network 구조는 앞으로 위의 간단한 그림과 같이 압축하여 표현할 것.
빨간 화살표(loop)는 recurrent의 의미를 내포한다.
RNN - Applications

그래서, 그러한 RNN은 여러 용도로 사용되는데, 각 용도마다 RNN의 구조가 달라진다. 여기에서는 이에 대해 간략하게만 소개한다.
- one to one: 가장 기본적인 RNN 구조
- one to many: Image Captioning (하나의 이미지 → 문장(시계열 데이터))
- many to one: Sentiment Classification (문장 → 문장의 분위기(긍정적/부정적 등))
- many to many (1): Machine Translation (영어 문장 → 한글 문장 으로 번역 등)
- many to many (2): Video classification in frame level (영상 → 각 프레임마다의 classification)
RNN - Training

Recurrent한 RNN 구조를 풀어 보면 위와 같은 형태이다.
여기에서 각 Time에 대한 $U, V, W$와 같은 matrix parameter들을 학습해야 하는 것.

다시 압축된 구조로 가져오면 위와 같다.
각 식과 항에 대한 부연 설명을 하자면,
$h_t$ 는 $t$시간에서의 state. $x_t$는 $t$시간에서의 input. $\hat y_t$는 output.
$\hat y_t = \phi(Vh_t)$ 에서의 $\phi$ 와, $h_t=\psi(Ux_t+Wh_{t-1})$ 에서의 $\psi$는 nonlinear activation function들.
(sigmoid, tanh, ReLU, …output layer에서 multiclass라면 softmax라던가. etc.)
이러한 구조의 Network에서 $U, V, W$와 같은 parameter를 학습하는 것이다.
forward propagation을 통한 계산은 왼쪽 식을 따라 진행하면 됨.

학습 과정은 이전까지의 NN 학습과 마찬가지로, Backpropagation을 이용하여 진행한다.
ANN, CNN에서와 같은 방식으로 진행하면 되는데, 시간 축이 새로 생겼기 때문에 Network가 기하급수적으로 복잡해져 학습에 시간이 오래 걸릴 것이다. (당연히, parameter가 엄청나게 많아졌기 때문.)