Reference
https://iai.postech.ac.kr/teaching/machine-learning
https://iai.postech.ac.kr/teaching/deep-learning
위 링크의 강의 내용에 기반하여 중요하거나 이해가 어려웠던 부분들을 정리하여 작성하였고,
모든 강의 슬라이드의 인용은 저작권자의 허가를 받았습니다.
또한, 모든 내용은 아래 Notion에서 더 편하게 확인하실 수 있습니다.
>>노션 링크<<
Least Square Solution

위와 같이 선형연립방정식 꼴에서,
unknown(변수)의 개수보다 constraint(방정식)의 개수가 더 많다면
⇒ matrix A의 꼴은 skinny하고, 이 때 일반적으로 solution이 존재하지 않음(해가 없다.)
이 때 column vector의 시각으로 보면, $\vec{a_1}$, $\vec{a_2}$를 $x_1, x_2$라는 coefficient(계수)로 선형결합 시킨 것이다.
이를 기하학적으로 생각하면, $\vec{a_1}$, $\vec{a_2}$로 span된 평면에 $\vec{b}$가 포함되지 않는다는 것을 의미.

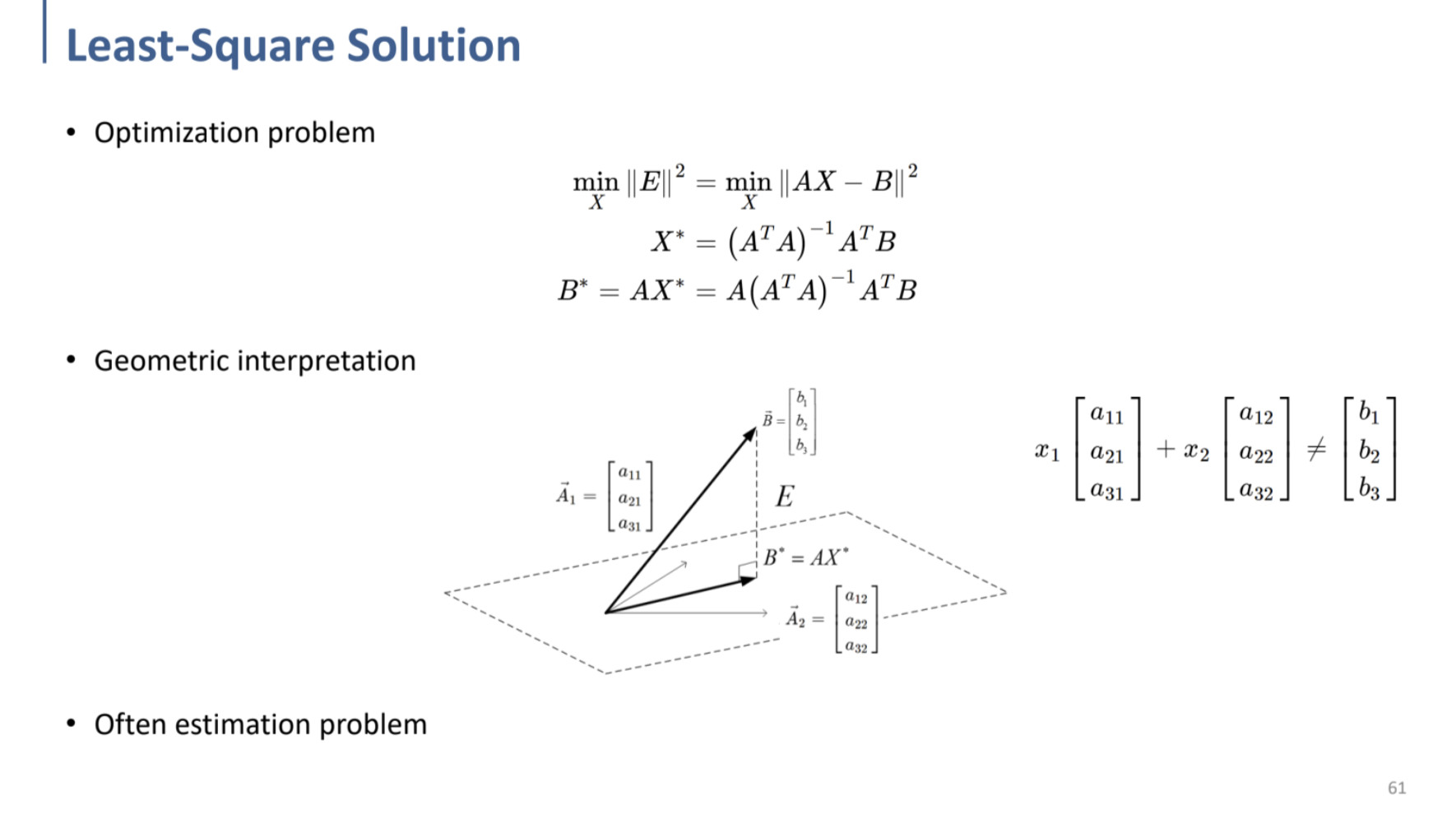
해를 구할 수는 없으나, 그러한 $\vec{b}$에 가장 가까운(error가 적은) $x_1, x_2$는 구할 수 있을 것.
이 때 2nd norm을 이용해 square error를 정의하고(또는 1st norm을 이용한 error → ||E||),
error의 min을 구하는 문제로 바꾸는 것이다. ( == 최적화 문제.)
Orthogonal Projection
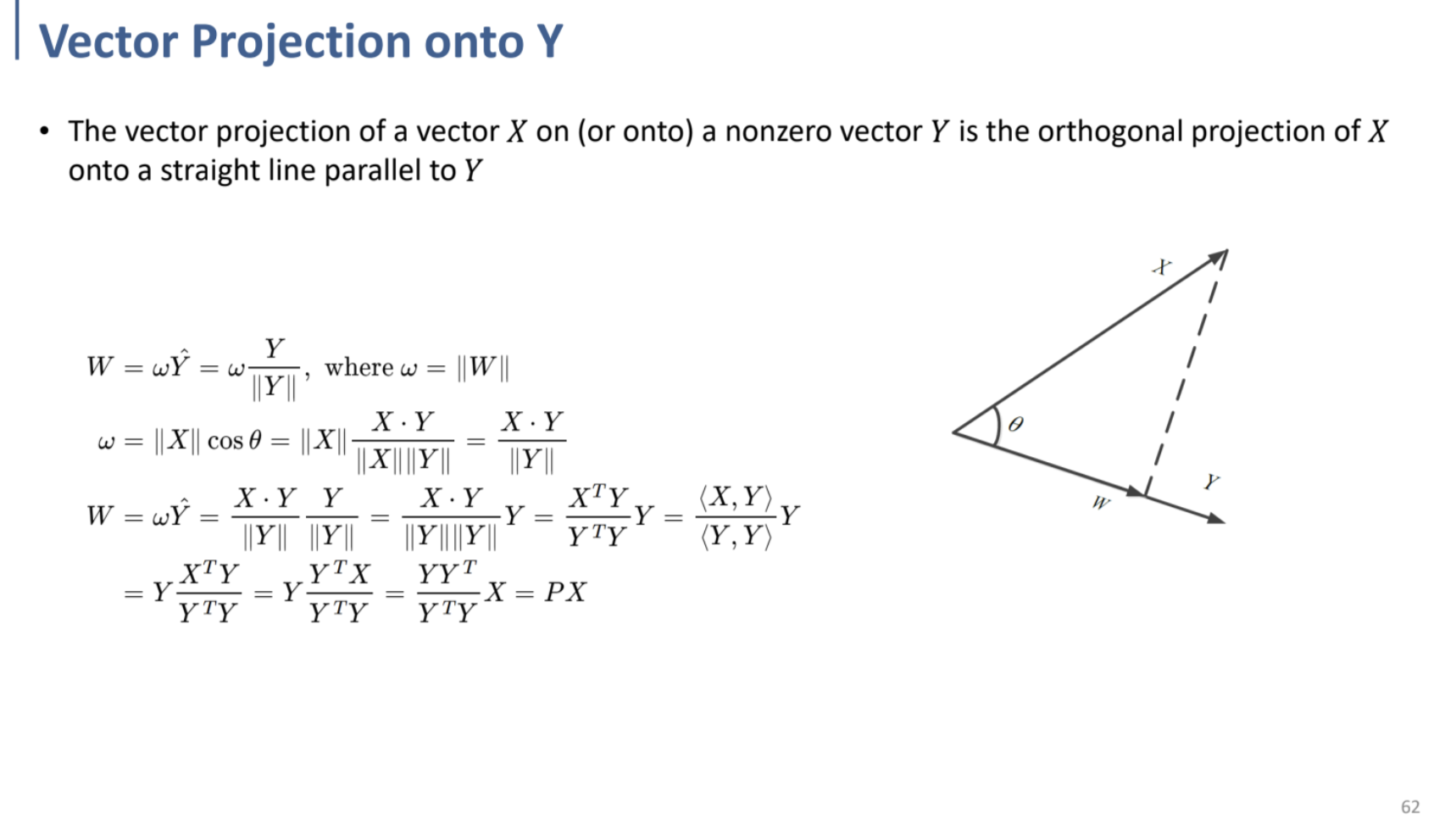

** 평면에 대한 직교투영으로 넘어가기 전, 한 벡터에 대한 직교투영에 대해 짚고 넘어가자.
X→Y로의 orthogonal projection(직교투영)에서,
X를 Y 방향으로 직교투영하게 되면, Y와 동일한 방향의, 크기가 다른 W vector를 얻게 된다.
이 때의 $\omega$ ($W = \omega\frac{Y}{||Y||}$), 또는 W vector가 되는 Y의 계수 $\frac{<X,Y>}{<Y, Y>}$가 뜻하는 것은 X, Y 사이의 각도이자, X, Y의 유사도(방향성의 유사도) 인 것이다.

다시 돌아와서, 결국 $x_1, x_2$를 구하는 문제는
$\vec{A_1}, \vec{A_2}$로 span된 subspace에 $\vec{B}$를 orthogonal projection시킨 vector를 만드는 $x_1, x_2$를 구하는 문제인 것이다.
⇒ 주어진 $A$에 대해, $B^* = AX^*$를 만족할 수 있는 $X^*$를 구하는 것.
(이 때 $AX^*-B = E$, $A\perp E$, $A^TE=0$ 이므로,
$A^T(AX^*-B)=0$ 이며, 이후 왼쪽 식 전개과정.)
이렇게 구해진 $X^*$가 Least Square Method(최소자승법)의 solution ⇒ regression에 이용.