Reference
https://iai.postech.ac.kr/teaching/machine-learning
https://iai.postech.ac.kr/teaching/deep-learning
위 링크의 강의 내용에 기반하여 중요하거나 이해가 어려웠던 부분들을 정리하여 작성하였고,
모든 강의 슬라이드의 인용은 저작권자의 허가를 받았습니다.
또한, 모든 내용은 아래 Notion에서 더 편하게 확인하실 수 있습니다.
>>노션 링크<<
Keywords
- Overfitting
- Regularization
- Ridge, Lasso
Overfitting

주어진 input, output - (training dataset)으로부터 optimizing을 달성하는 $\theta$값을 찾는 문제를 풀다 보면, 결국 그러한 특정 데이터에 맞춰진 model이 만들어지게 된다.
⇒ 이렇게 되면, training dataset에 대한 optimizing을 달성하여, training data에 대한 loss는 최소화될 수 있으나, testing dataset(new data)에 대해서는 prediction loss가 점차 증가하는 방향으로 나아가게 된다.
(이를 generalization error라 한다.)
이러한 현상을 Overfitting - 특정 data에 over하게 fit(= train)되는 것. - 이라 하며,
이를 해결하기 위한 방식을 Regularization이라 한다.
Regularization

Regularization을 달성하는 방법에도 여러 가지가 존재하는데, 위의 PDF에서도 알 수 있듯,
- 더 간단한 함수를 사용하여 model을 만들어나가는 방법이 있고, (ex. polynomial이라면 최고차수를 낮추고, RBF function의 개수를 줄이는 등)
- parameter의 크기를 줄이는 방법이 있다. (coefficient의 크기를 줄임)
Overfitting이 되어 모델이 복잡해지면, parameter(coefficient)의 크기(magnitude)가 증가하는 경향을 띔. → 반대로 이 크기를 줄이면, Regularization을 달성할 수 있음.

두 번째 방법인 parameter $\theta$의 크기를 줄이기 위해, Optimization function을 위와 같이 변경하여 multi-objective optimization problem으로 변경할 수 있다.
기존의 real output data와 prediction 간의 차이의 2nd norm을 minimize하는 항에
+ 새로운 항 $\lambda||\theta||^2_2$ (parameter $\theta$의 2nd norm의 제곱)을 추가함으로써,
전체 식을 minimize하는 문제로 변경되게 된다.
따라서, parameter의 크기를 줄일 수 있게 된다.
⇒ 식을 minimize하는 과정에서, 위의 PDF에서의 $RSS(\theta)$와 $\lambda||\theta||^2_2$ 사이의 trade-off가 일어나게 된다.
measure of fit(RSS)를 줄이게 되면 (실제 output과 prediction 사이의 차이를 줄이게 되면) 필연적으로 parameter $\theta$ 값이 늘어나게 될 것이고,
반대로 $\lambda||\theta||^2_2$를 줄이게 되면 RSS가 늘어나, training data에 대한 output-prediction loss가 증가하게 되는 것이다.

참고로 이 multi-objective optimization fucntion의 두 번째 항은 shrinkage penalty라 부르며,
위에서도 말했듯, parameter $\theta$값을 0으로 만드려는 경향이 있다.
이 때의 $\lambda$ 값은 tuning parameter (hyperparameter의 일종)이며,
이 $\lambda$가 클수록, $\theta$를 작게 만드려는(0으로 만드려는) 경향성이 더 커지고, 반대로 작을수록 parameter를 작게 하려는 힘이 약해진다.
(이는 당연히, $\lambda$가 클수록 두번째 항이 더 큰 폭으로 커지기 때문에..)
그리고 이러한 2nd norm을 이용한 Regularization을 Ridge라 한다!
Ridge, Lasso

L2 norm (Ridge)가 아닌, L1 norm (Lasso)를 이용한 Regularization을 수행할 수도 있다.

Linear Regression에서 L1 norm을 사용하는 것이, outlier에 대한 penalty가 적었던 것을 상기하자.
(L2 norm은 거리의 제곱을 이용하므로, outlier에 대한 영향이 커짐.)
Regularization에서 L1 norm을 이용하는 것은 경우가 다른데,
위의 그래프에서 확인할 수 있듯, Ridge와 다르게, Lasso에서는
”feature selection” 효과를 수행하는 것을 볼 수 있다.
⇒ LASSO 측에서는 Regularization의 결과로 $\theta=0$ 값인 basis(feature)가 여러 개 존재하는 것을 확인할 수 있다.
Lasso Regularization에서는 중요한 feature에 대한 parameter만 남겨두고, 중요하지 않은 feature에 대한 parameter를 0으로 만들어 없애는 역할을 수행하여, feature selection과 같은 효과를 얻어낼 수 있다는 장점을 가진다.

따라서, RSS항과 L1 norm을 이용한 penalty항의 합으로 이루어진 Optimization function에 대한 minimize를 수행하면,
모든 feature(basis)가 살아있는 상태의 full model에서 - penalty항에 의해 각 feature의 parameter(coefficient)가 0으로 shrink되면서, 몇몇 feature가 삭제되는 효과를 내는 것이다.
이에 따라, optimize가 진행된 이후에 coefficient가 0이 되지 않은 feature들이 select되는 결과를 낳는다.
(Sparsity, 희소성 유도)

그렇다면, 왜 Lasso가 특정 feature에 대한 parameter(coefficient)를 0으로 shrink하는 것인가?
Ridge는 왜 그러한 효과를 내지 못하는가? - 에 대해서는 기하학적으로 확인하면 이를 이해할 수 있다.
우선 아래쪽 PDF를 확인하자.
맨 위의 두 식은 unbounded optimization problem으로 정의할 수 있다.
이를 아래처럼 parameter의 constraint를 정의하여 다른 문제로 바꾼다고 생각해보는 것이다.
Regularization이 결국 parameter $\theta$ 값을 줄이는 것이므로, 이에 대한 최댓값(upper bound)을 임의로 설정하여 생각해 보자는 것이다.
이 예시에서의 그래프는 2차원 공간에서의 예시를 시각화한 것이다. (= parameter의 개수가 2개인 경우)
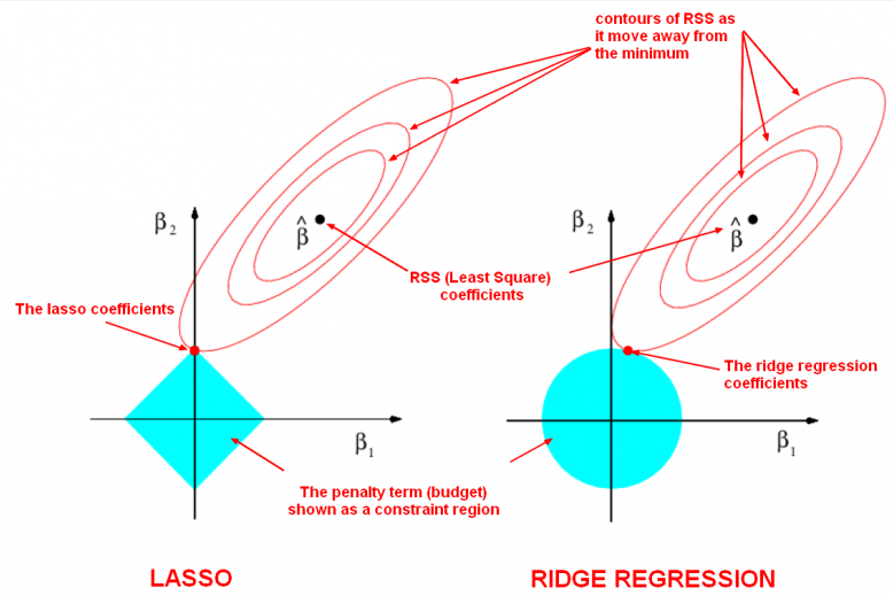
그렇게 되면, 그래프의 파란색 영역이 parameter의 upper bound를 표시하는 영역(feasible region)이고,
빨간 타원으로 표시된 것이 RSS항이다.
(이 때, L1 norm인지 L2 norm인지는 거리를 정의하는 도구의 역할을 하게 되는 것이다. L1 norm으로 거리를 정의하였다면, 마름모꼴이 되는 것은 쉽게 생각할 수 있다.)
결국 파란색 영역 (feasible region) 안쪽에 들어가는 parameter $\theta$ 중, $||\Phi\theta-y||^2_2$를 minimize하는 $\theta$를 결정하면 되는 것인데, 여기서 L1 norm의 경우에는 마름모의 꼭지점에 해당하는 곳에서 접하게 된다.
(RSS를 의미하는 빨간 타원이 $\hat\beta$에 가까울수록 minimum에 가까운 것. 멀수록 output data-prediction의 차이가 커짐을 의미하는데, 기하학적으로 그러한 차이와 parameter의 크기 사이에 trade-off가 일어남을 확인할 수 있다.)
그래프에서 볼 수 있듯 꼭짓점은 한 parameter값이 0이 되는 부분이고, 그렇기 때문에 feature selection이 일어나게 되는 것이다.