Reference
https://iai.postech.ac.kr/teaching/machine-learning
https://iai.postech.ac.kr/teaching/deep-learning
위 링크의 강의 내용에 기반하여 중요하거나 이해가 어려웠던 부분들을 정리하여 작성하였고,
모든 강의 슬라이드의 인용은 저작권자의 허가를 받았습니다.
또한, 모든 내용은 아래 Notion에서 더 편하게 확인하실 수 있습니다.
>>노션 링크<<
Keywords
- Linear Regression
- Least Square Solution
- L1, L2 norm
Linear Regression

가장 간단한 모델인 선형 모델에서부터 보자면,
$y_i$를 가장 잘 predict(예측)하기 위한 linear model인 $f(\theta)$ (여기선, $\theta_0, \theta_1$)을 찾는 것
⇒ 이것이 Linear Regression의 의의.
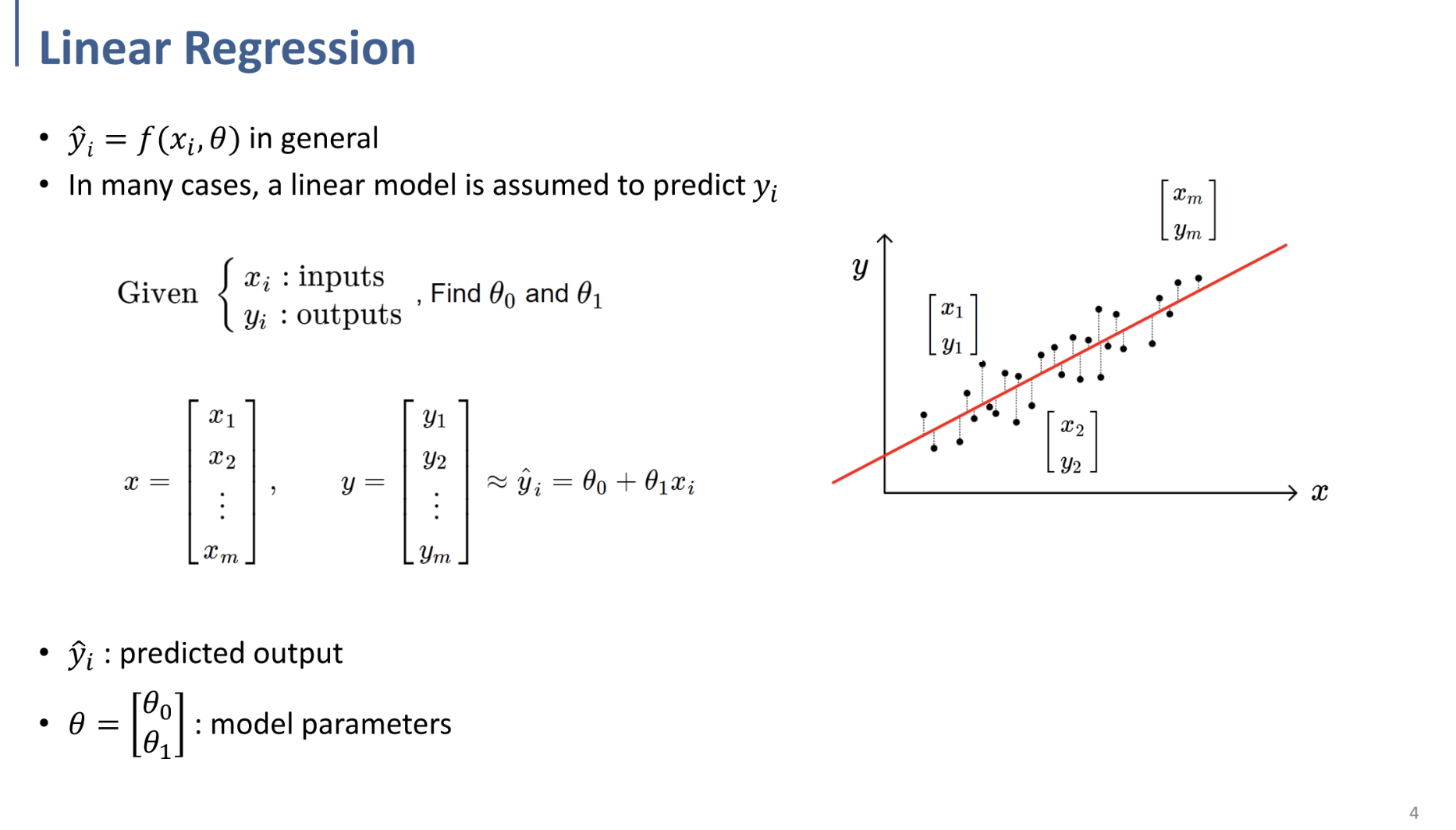

주어진 input, output으로부터 $\theta_0, \theta_1$ 찾기.
어떻게 찾느냐?
⇒ Optimization Problem.
(Prediction value - real value) = Error(norm)이고, → 이것의 제곱을 object function으로 설정.
그러한 error가 min이 되는 $\theta_0, \theta_1$ 찾기.
$min\sum\limits_{i=1}^n(\hat{y}_i-y_i)^2$ 을 만족하도록 하는 $\theta$값을 찾는 것!

위 페이지와 같이 function을 저런 matrix*vector 형식으로 변환할 수 있게 됨. (읽어보면 간단)
⇒ Least Square Solution을 상기할 것.

따라서 이는 Optimization 문제로 치환됨.
* solution $\theta^*$가 나오는 과정은 Least Square Solution 파트를 참고할 것.
[ML/DL 스터디] <Linear Algebra - 2> Least Square Solution, Orthogonal Projection
[ML/DL 스터디] <Linear Algebra - 2> Least Square Solution, Orthogonal Projection
Referencehttps://iai.postech.ac.kr/teaching/machine-learninghttps://iai.postech.ac.kr/teaching/deep-learning위 링크의 강의 내용에 기반하여 중요하거나 이해가 어려웠던 부분들을 정리하여 작성하였고,모든 강의 슬라이
wondev.tistory.com

Least Square Solution(최소자승법)의 관점에서 바라보면 위와 같게 됨.
$\vec{A_1},\vec{A_2}$를 통해 span되는 평면에서, $\theta$값($\vec{X}$)에 따라 평면 위의 모든 vector를 표현할 수 있고,
이 때, $\vec{B}$가 span된 평면 밖에 있으므로, $\vec{B}$를 평면상에 projection 값에 해당하는 $\vec{B}^*$를 만드는 $\vec{X}^*$를 구하는 것임을 다시 상기하자.
L2 Norm, L1 Norm

** 위에서 말했듯, L1 norm도 거의 동일한 Regression의 결과를 만들 수 있다. 둘 다 사용할 수 있음.
그렇다면 왜 L2 norm을 사용하는가? 에 대해서는 data 중 outlier가 존재하는 경우를 확인하면 파악할 수 있다.

(CVX를 사용하여 Linear Regression을 수행한 결과를 plot한 것.)
⇒ L2 norm은 outlier에서 error가 크기 때문에, 이를 제곱하면 더욱 커짐. 따라서 outlier의 영향을 크게 받음.
따라서, L1 norm을 사용하는 것이 outlier에 대한 penalty가 줄어듬.
** 최종 정리
- Linear Regression ⇒ Optimization 문제로 치환 가능
- 이를 푸는 방법
- Projection, Least Square Solution을 이용
- CVXPY를 이용 (convex function → optimal solution)
- Gradient Descent를 이용 (이 페이지에서 나오지 않았지만, 그대로 적용 가능. 알듯이.)
- L1, L2 norm과 그것이 결과에 끼치는 영향, 차이.