Reference
https://iai.postech.ac.kr/teaching/machine-learning
https://iai.postech.ac.kr/teaching/deep-learning
위 링크의 강의 내용에 기반하여 중요하거나 이해가 어려웠던 부분들을 정리하여 작성하였고,
모든 강의 슬라이드의 인용은 저작권자의 허가를 받았습니다.
또한, 모든 내용은 아래 Notion에서 더 편하게 확인하실 수 있습니다.
>>노션 링크<<
Keywords
- Perceptron
- signed distance
Signed Distance
(앞에서의 perceptron의 기본적인 개요에 대해서는 생략.)
⇒ discrete한 값의 y에서의 Classification.
boundary를 찾기 위한 여정.
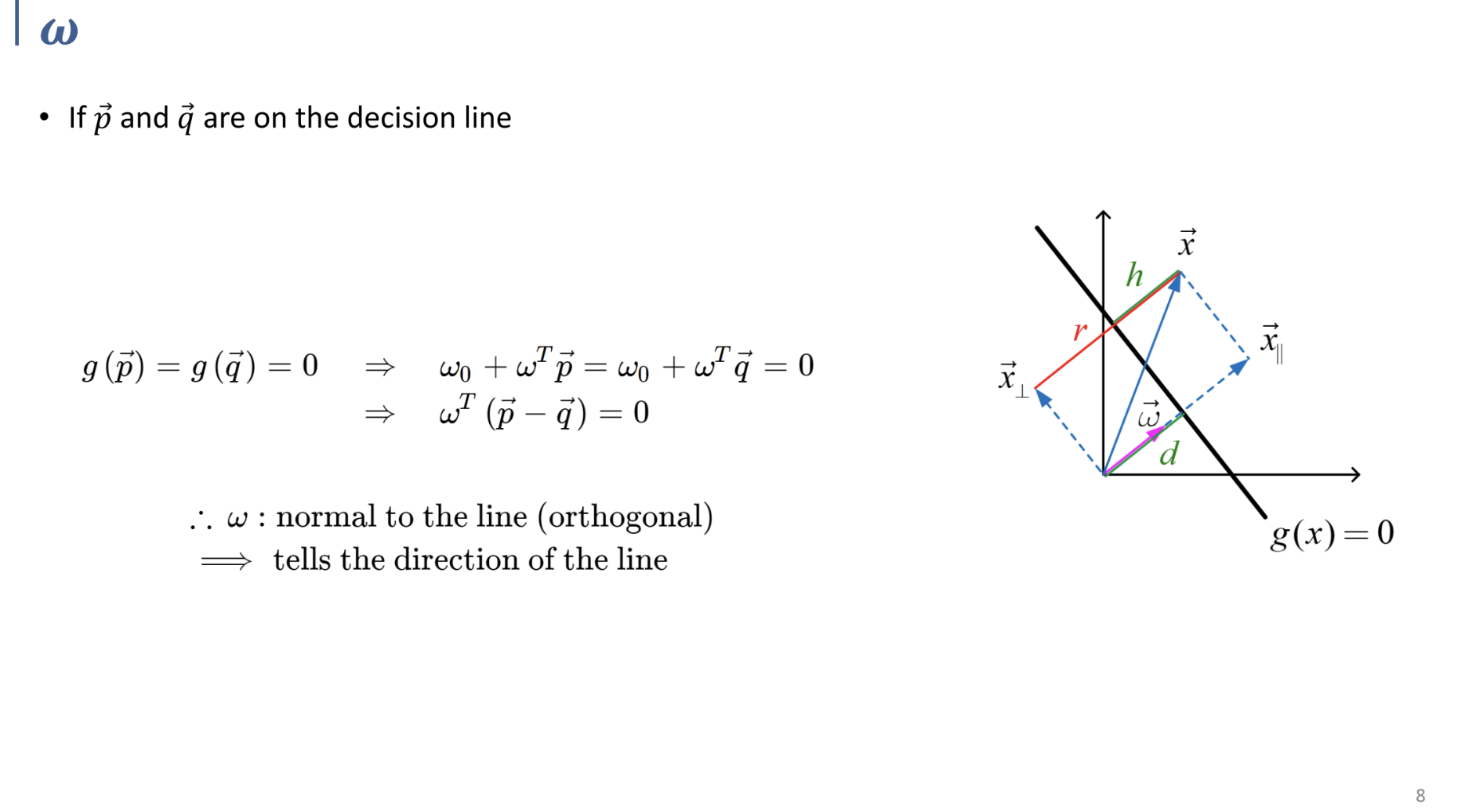
평면 상에서 $\vec\omega$가 위의 이유로 직선에 대한 법선벡터(orthogonal함)임을 확인할 수 있다.


그리고 위의 두 식을 통해, 원점으로부터 직선의 거리 $d$ 와 직선으로부터 임의의 한 점까지의 거리 $h$ 에 대한 $\omega$ 로 나타낸 식을 구할 수 있다.
(앞의 pdf에서는 $x$가 직선 위의 임의의 한 점, 뒤의 pdf에서는 원점→평면 상의 임의의 점인 벡터 $\vec x$를 정의하고 계산. 식을 보면 어렵지 않게 이해할 수 있을 것.)
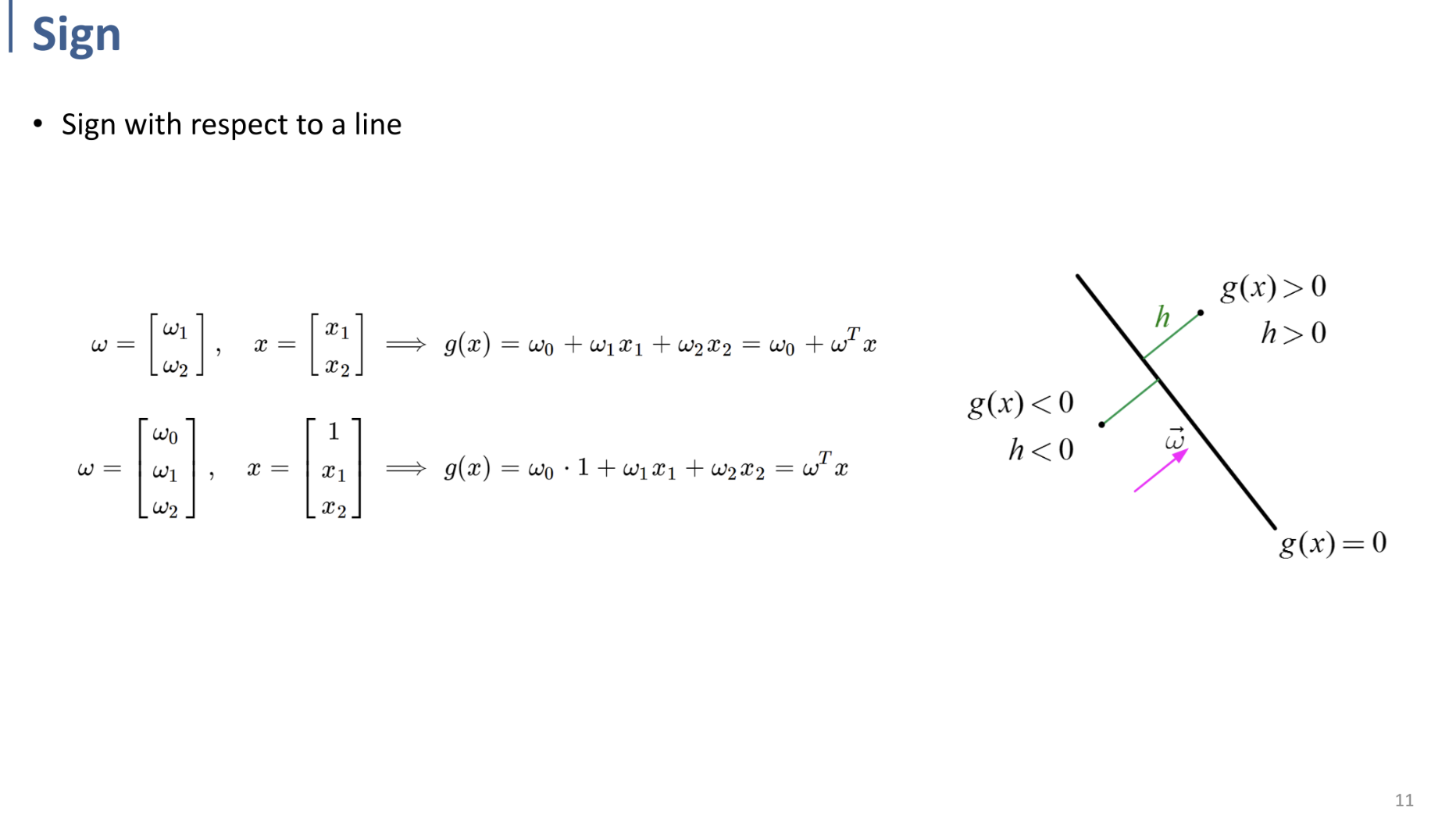
$\vec\omega$의 방향에 따라, 같은 방향 평면쪽의 모든 점에 대해 $g(x)>0, h>0$ 이며,
반대 방향 평면 쪽의 모든 점에 대해 $g(x) < 0, h<0$ 이다.
(이는 w와 inner product(내적)했을 때 사이각이 90도 미만이면 양수, 90도 초과 180도 미만이면 음수이기 때문임을 직관적으로 이해할 수 있다.)
결국 $g(x) = \omega^Tx = 0$ 이라는 직선이 전체 평면을 둘로 나누는 binary classification boundary가 된다.
따라서 특정 $x$ (input)에 대해, $g(\omega^Tx)$ 의 부호를 계산하면 그 input에 대한 class를 결정할 수 있게 되는 것이다.
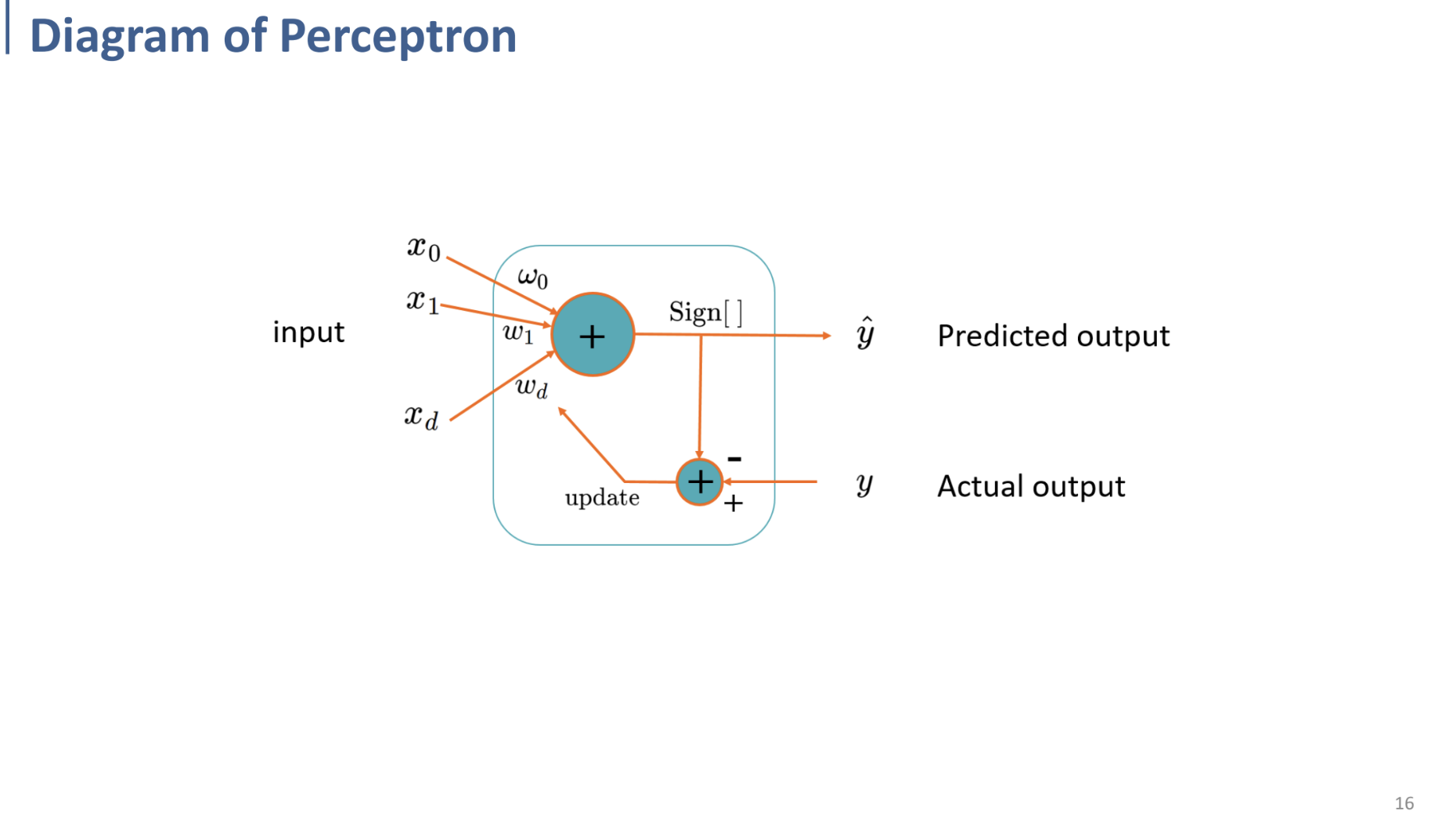
Perceptron
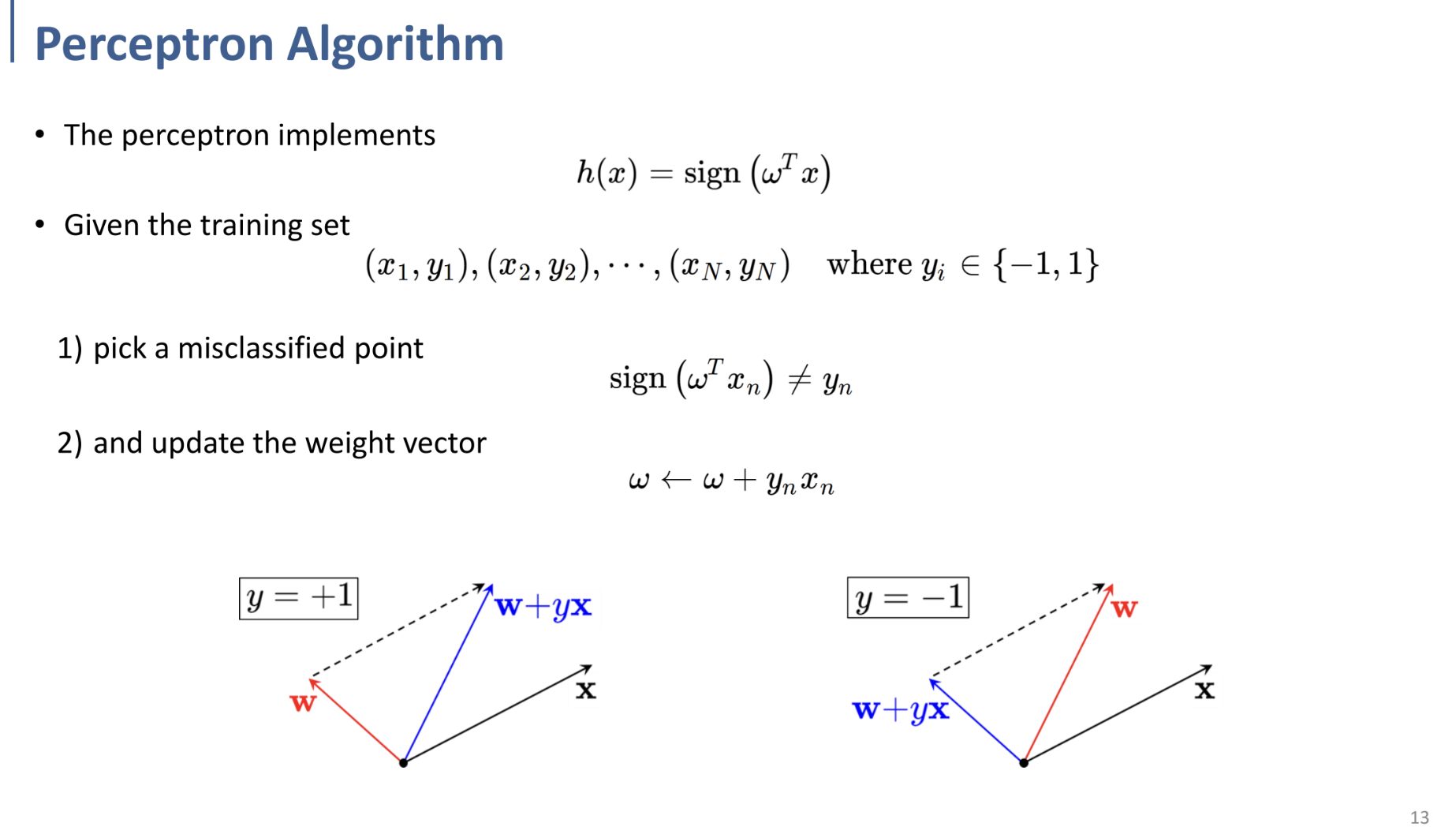
앞의 기반들을 알고 나서, Perceptron에서 어떻게 parameter(weights, $\omega$)를 찾을 것인가에 대한 문제를 확인할 수 있다.
- perceptron 함수 $h(x) = sign(\omega^Tx)$ 를 정의하고,
- 모든 training data에 대해 이 함수를 적용한 후,
- prediction의 결과 class와 output의 실제 class가 다르다면,
- $\omega ← \omega + y_nx_n$을 통해 weight를 업데이트한다.
* 데이터가 선형 분리 가능할 경우, 이 규칙을 사용하면 Perceptron이 유한한 횟수의 업데이트 후에 수렴함이 수학적으로 증명되어 있다.
여기서 왜 $\omega ← \omega + y_nx_n$라는 뜬금없는 식을 통해 weight을 업데이트하는 지에 대해서는 PDF 아래쪽의 그림을 보면 대략 이해할 수 있다.
왼쪽의 그림에서 기존의 $\mathbf w$를 기준으로 직선을 상상해 보면, $\mathbf x$는 직선 반대쪽에 있으므로 $y=-1$로 misclassified된 것이다.
그렇기 때문에 파란색의 새로운 벡터로 갱신하여 다시 그 벡터를 기준으로 직교하는 직선을 상상해 보면, x가 같은 방향에 존재하여 $y=+1$로 잘 classify되는 것을 확인할 수 있다.
위의 로직을 수행하면, 적어도 weight을 갱신한 해당 data point에 대해서는 항상 perceptron이 잘 동작(잘 분류)한다.
이 과정을 misclassify되는 data point가 존재하지 않을 때까지 weight을 갱신시켜 나가며 반복하는 것이 Perceptron Algorithm이다.
식을 보면 결국 이는 perceptron의 loss function에 대한 음수 방향으로 가중치를 조정하는 간단한 경우의 gradient descent라고 볼 수 있다.